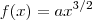por Mendes » Dom Ago 23, 2015 15:10
por Mendes » Dom Ago 23, 2015 15:10
Enunciado:
Um engenheiro resolveu construir uma escada na sua casa que possuia dois andares, mas teve dúvida na construção do corrimão porque as duas escadas formavam dois arcos. Sabendo que o corrimão começa com a escada e que de uma escada para outra o arco faz um giro. Determine a função, os pontos de início e fim de cada arco para cada andar, sabendo que a altura não pode ultrapassar 1m e que esses dois arcos formam uma parábola semicúbica e que o comprimento não pode ultrapassar 5 unidades de comprimento.
Eu sei que terei que somar a integral das duas funções, e também sei que as integrais vão de 0 a 1 e de 1 a 2 respectivamente, para respeitar a altura de 1m.
Pela definição de parábola semicúbica temos que
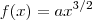
Fonte:
https://pt.wikipedia.org/wiki/Par%C3%A1 ... %C3%BAbicaSegue em anexo um esboço do que eu consegui deduzir num gráfico. Não sei se está certo, mas foi o que eu tentei.
Dúvida: Eu queria saber como deduzir as funções solicitadas? Não sei por onde começar

- Anexos
-
![questao[1].jpg (815.12 KiB) Exibido 1442 vezes questao[1].jpg](./download/file.php?id=2325&t=1)
- Esboço de gráfico
-
Mendes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Ago 23, 2015 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas/Sistemas de Informação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- comprimento do arco
por liviabgomes » Seg Mai 30, 2011 16:11
- 10 Respostas
- 6248 Exibições
- Última mensagem por liviabgomes

Qua Jun 01, 2011 15:03
Cálculo: Limites, Derivadas e Integrais
-
- comprimento de arco
por manuoliveira » Ter Out 23, 2012 19:43
- 0 Respostas
- 1313 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 19:43
Cálculo: Limites, Derivadas e Integrais
-
- comprimento do arco
por VenomForm » Seg Mai 20, 2013 13:29
- 0 Respostas
- 1248 Exibições
- Última mensagem por VenomForm

Seg Mai 20, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
-
- Calculo do comprimento do arco.
por brunojorge29 » Seg Abr 23, 2012 11:21
- 3 Respostas
- 2967 Exibições
- Última mensagem por Russman

Seg Abr 23, 2012 22:32
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento do arco!! Urgente!!
por manuoliveira » Ter Out 23, 2012 20:34
- 4 Respostas
- 3500 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 21:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.