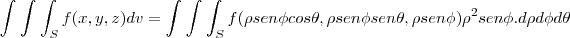por fatalshootxd » Ter Mar 31, 2015 00:43
por adauto martins » Sáb Abr 04, 2015 16:13
,onde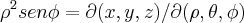 
q. eh o jacobiano na mudança de variaveis...
,vamos encontrar o ponto de intersecçao dos solidos,ou seja o valor de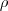 
...![\rho =\sqrt[]{3({x}^{2}+{y}^{2})}\Rightarrow {\rho}^{2}/3={x}^{2}+{y}^{2}](/latexrender/pictures/95c36d10979e4d3f1371bd382a31fbc3.png "\rho =\sqrt[]{3({x}^{2}+{y}^{2})}\Rightarrow {\rho}^{2}/3={x}^{2}+{y}^{2}")
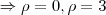e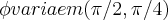 
,pois o cone de revoluçao tem raios e altura iguais...logo![\int_{0}^{3}{\rho}^{2}/{\rho}^{2}.\int_{\pi/2}^{\pi/4}sen\phi.\int_{0}^{2\pi}d\theta d\phi d\rho=\int_{0}^{3}}.\int_{\pi/2}^{\pi/4}sen\phi.2\pi.d\rho.d\phi=\int_{0}^{3}}(-(cos\pi/2-cos\pi/4).2\pi d\rho=4\pi.\sqrt[]{2}/2\int_{0}^{3}}d\rho=2.3.\sqrt[]{2}\pi=6.\sqrt[]{2}\pi](/latexrender/pictures/dd247862c54b336cac1c641757e3c102.png "\int_{0}^{3}{\rho}^{2}/{\rho}^{2}.\int_{\pi/2}^{\pi/4}sen\phi.\int_{0}^{2\pi}d\theta d\phi d\rho=\int_{0}^{3}}.\int_{\pi/2}^{\pi/4}sen\phi.2\pi.d\rho.d\phi=\int_{0}^{3}}(-(cos\pi/2-cos\pi/4).2\pi d\rho=4\pi.\sqrt[]{2}/2\int_{0}^{3}}d\rho=2.3.\sqrt[]{2}\pi=6.\sqrt[]{2}\pi")
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)