 por wellkirby » Qui Mar 19, 2015 19:25
por wellkirby » Qui Mar 19, 2015 19:25
Olá Pessoal,
Estava fazendo uma lista e não consegui entender essa questão:
"Ao meio-dia, um navio A está 100 km a oeste do navio B. O navio A está navegando para o sul a 35 km/h, e o navio B está indo para o norte a 25 km/h. Quão rápido estará variando a distância entre eles às 4 horas da tarde?"
Alguém poderia me explicar? Tenho um problema com taxas relacionadas, se alguém tiver uma boa video aula ou material para indicar, ficaria muito agradecido
Att
-
wellkirby
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Out 01, 2014 23:56
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Baltuilhe » Sex Mar 20, 2015 10:30
por Baltuilhe » Sex Mar 20, 2015 10:30
Bom dia!
Podemos ver que, se o navio A estiver no ponto (0,0) o navio B estará no ponto (100,0).
Equação para o navio A:
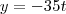
Ponto A (posição atualizada do navio): (0,-35t)
Equação para o navio B:
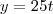
Ponto B (posição atualizada do navio): (100,25t)
Distância entre os dois (ao quadrado):
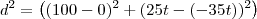
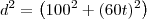
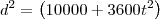
Distância entre os dois:

A taxa de variação é a derivada da função. Derivando-a para t=4h, teremos:
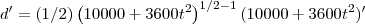
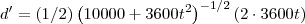
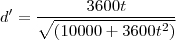
Substituindo t=4h:
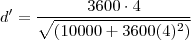
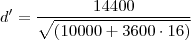
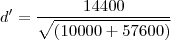
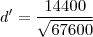
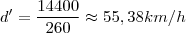
Como o valor é positivo, estão se afastando deste valor.
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada]- Taxas de variação
por Ana_Rodrigues » Qui Fev 23, 2012 21:06
- 1 Respostas
- 1297 Exibições
- Última mensagem por LuizAquino

Qui Fev 23, 2012 21:33
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] taxas relacionadas
 por math13 » Seg Abr 06, 2015 16:02
por math13 » Seg Abr 06, 2015 16:02
- 0 Respostas
- 1029 Exibições
- Última mensagem por math13

Seg Abr 06, 2015 16:02
Cálculo: Limites, Derivadas e Integrais
-
- taxas relacionadas derivada
por JoaoLuiz07 » Dom Fev 07, 2016 14:20
- 1 Respostas
- 3752 Exibições
- Última mensagem por adauto martins

Seg Fev 08, 2016 14:43
Cálculo: Limites, Derivadas e Integrais
-
- taxas relacionadas derivada
por JoaoLuiz07 » Seg Fev 08, 2016 16:17
- 1 Respostas
- 3267 Exibições
- Última mensagem por adauto martins

Dom Fev 28, 2016 13:11
Cálculo: Limites, Derivadas e Integrais
-
- [Taxas Relacionadas]
por Ana_Rodrigues » Seg Nov 14, 2011 10:02
- 2 Respostas
- 4598 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 12:19
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


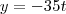
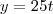
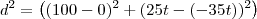
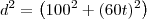
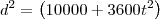

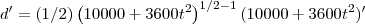
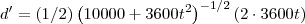
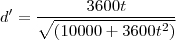
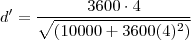
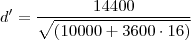
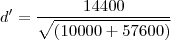
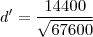
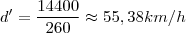



 , avisa que eu resolvo.
, avisa que eu resolvo.

