 por killerkill » Seg Mar 16, 2015 17:24
por killerkill » Seg Mar 16, 2015 17:24
Pessoal, estou tentando entender a ideia intuitiva de um campo vetorial conservativo pro caso de integrais de linha. Meus conceitos estão muito embaralhados e gostaria da ajuda de alguém pra ajudar a organiza-los. Pelo que eu entendi até agora no meu curso, a integral de linha pode ser interpretada de varias formas, como uma área sobre uma curva até a função (espécie de cortina), como densidade em determinado ponto da curva e na parte onde estou tendo mais dificuldades, em um campo vetorial. Nessa ultima eu me embolo completamente quando se envolve o conceito de campo conservativo. Em uma curva fechada C1, imerso num campo conservativo, se selecionarmos um ponto "A" pertencente a essa curva e realizarmos uma volta completa na curva, a integral de linha (ou deveria eu dizer trabalho?) sobre essa curva é igual a zero. Ou seja, independe do caminho. Acho que não entendi o porquê. O único caso que consegui imaginar tentando fazer uma lógica foi o seguinte: imaginei uma curva em 3 dimenões imersa no campo gravitacional. Se eu partir de um ponto P1 na parte mais alta da curva(mais distante do centro do campo) e largar uma partícula imaginária, a força gravitacional irá atuar até que ela chegue ao ponto mais baixo da curva realizando um trabalho W1. Pro caso dessa partícula retornar ao ponto P1 o trabalho seria W2, de mesma intensidade que W1 porém agora contrária ao campo, ou seja, com valor negativo. Nesse caso, intuitivamente fica claro pensar que essa integral seria igual a zero. Essa ideia é correta?
-
killerkill
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Ago 09, 2011 22:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eg. Elétrica
- Andamento: cursando
 por adauto martins » Sex Mar 20, 2015 12:39
por adauto martins » Sex Mar 20, 2015 12:39
seja
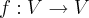
,onde V um espaço vetorial sobre um corpo K...
f e dito conservativo
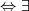
uma funçao
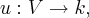
tal q.
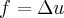
,onde
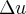
e o gradiente u em V...usando o teorema de stokes,mostra-se q. ...
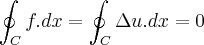
,ou seja vai independer dos pontos inicias e finais,ou indepedente do caminho...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo Vetorial
por roger0196 » Seg Abr 04, 2011 15:02
- 6 Respostas
- 5393 Exibições
- Última mensagem por Jackie

Ter Abr 26, 2011 20:20
Geometria Analítica
-
- Calculo Vetorial
por Renato Lima » Qua Abr 27, 2011 22:21
- 1 Respostas
- 2093 Exibições
- Última mensagem por LuizAquino

Qua Abr 27, 2011 23:12
Geometria Analítica
-
- GA e Calculo Vetorial
por camposhj » Sex Out 07, 2011 00:41
- 3 Respostas
- 2472 Exibições
- Última mensagem por LuizAquino

Sex Out 07, 2011 13:06
Geometria Analítica
-
- Cálculo Vetorial
por Jhenrique » Ter Jul 02, 2013 19:10
- 0 Respostas
- 1595 Exibições
- Última mensagem por Jhenrique

Ter Jul 02, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- cálculo vetorial
por fasaatyro » Sáb Mai 02, 2015 12:02
- 0 Respostas
- 1285 Exibições
- Última mensagem por fasaatyro

Sáb Mai 02, 2015 12:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



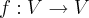 ,onde V um espaço vetorial sobre um corpo K...
,onde V um espaço vetorial sobre um corpo K...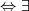 uma funçao
uma funçao 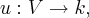 tal q.
tal q. 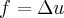 ,onde
,onde 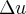 e o gradiente u em V...usando o teorema de stokes,mostra-se q. ...
e o gradiente u em V...usando o teorema de stokes,mostra-se q. ...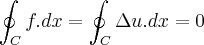 ,ou seja vai independer dos pontos inicias e finais,ou indepedente do caminho...
,ou seja vai independer dos pontos inicias e finais,ou indepedente do caminho...


 , avisa que eu resolvo.
, avisa que eu resolvo.

