![f(x)= [cos x], -\pi \leq x \leq \pi f(x)= [cos x], -\pi \leq x \leq \pi](/latexrender/pictures/6d2672b0e6524334517a98ed45e26c9b.png) . (Os colchetes simbolizam a função piso)
. (Os colchetes simbolizam a função piso)a) Calcule cada limite, se existir.
I)
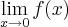
II)
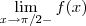
III)
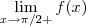
IV)
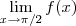
b) Para quais valores de a existe
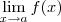 ?
?Sei que a função maior inteiro representa o maior inteiro que não ultrapasse o valor de X mas não consigo responder essa questão e não tenho o gabarito. Obrigado desde já!


![f(x)=cosx\Rightarrow \left[f(x) \right]=\left[cosx \right] f(x)=cosx\Rightarrow \left[f(x) \right]=\left[cosx \right]](/latexrender/pictures/a6654b1aa87894edcc9dbcc4ac19a9a8.png)
![\left[f(x) \right]\preceq \left[f(x) \right]\prec \left[f(x) \right]+1,p/\left[f(x) \right]\in Z \left[f(x) \right]\preceq \left[f(x) \right]\prec \left[f(x) \right]+1,p/\left[f(x) \right]\in Z](/latexrender/pictures/55ba575bf9c1de38cf4f8c6731589961.png) ,entao
,entao![\left[cox \right]\preceq cosx \prec \left[cosx \right]+1 \left[cox \right]\preceq cosx \prec \left[cosx \right]+1](/latexrender/pictures/13ee90b3145aa84f4c0c9ced41d2a821.png)
![\lim_{x\rightarrow 0}\left[cosx \right]\preceq \lim_{x\rightarrow 0}cosx\prec \lim_{x\rightarrow 0}cosx+1\Rightarrow \lim_{x\rightarrow 0}\left[cosx \right]=cos0=1 \lim_{x\rightarrow 0}\left[cosx \right]\preceq \lim_{x\rightarrow 0}cosx\prec \lim_{x\rightarrow 0}cosx+1\Rightarrow \lim_{x\rightarrow 0}\left[cosx \right]=cos0=1](/latexrender/pictures/b13c775b7b0b4405b61dc46eaba3a38e.png)
![\lim_{x\rightarrow {\pi/2}^{-}}\left[cosx \right]\preceq \lim_{x\rightarrow {\pi/2}^{-}}cosx=cos(\pi/2)=0 \lim_{x\rightarrow {\pi/2}^{-}}\left[cosx \right]\preceq \lim_{x\rightarrow {\pi/2}^{-}}cosx=cos(\pi/2)=0](/latexrender/pictures/6612b303fba0eb51c8b1adf775a0e002.png) ...
...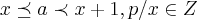

![\lim_{x\rightarrow a}\left[f(x) \right] \lim_{x\rightarrow a}\left[f(x) \right]](/latexrender/pictures/b9cfe93e359820cd9c7df3519c27f248.png) ,pois p/diferentes valores de x,o limite tem o mesmo valor...
,pois p/diferentes valores de x,o limite tem o mesmo valor...![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)