 por Fernandobertolaccini » Sex Dez 19, 2014 17:33
por Fernandobertolaccini » Sex Dez 19, 2014 17:33
Comprove que:
Se
![z=\frac{x^2+y^2}{\sqrt[]{x+y}} z=\frac{x^2+y^2}{\sqrt[]{x+y}}](/latexrender/pictures/613101109245f528c9bf809a7d5d3079.png)
, então
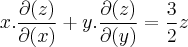
para y>-x
Como chegar neste resultado?
Muito obrigado !!
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Ter Dez 23, 2014 16:28
por adauto martins » Ter Dez 23, 2014 16:28
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:28
- 1 Respostas
- 2266 Exibições
- Última mensagem por adauto martins

Qui Dez 25, 2014 13:09
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:44
- 2 Respostas
- 2373 Exibições
- Última mensagem por adauto martins

Qua Dez 24, 2014 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Derivada com várias variáveis
por kryzay » Seg Mai 14, 2012 09:23
- 2 Respostas
- 2678 Exibições
- Última mensagem por kryzay

Seg Mai 14, 2012 10:58
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo para Funções de Várias Variáveis I
por ehrefundini » Ter Abr 29, 2008 23:16
- 1 Respostas
- 5890 Exibições
- Última mensagem por Neperiano

Dom Set 04, 2011 22:28
Pedidos de Materiais
-
- [Cálculo de várias variáveis] Problema de regra da cadeia
por Hoteri » Seg Dez 05, 2016 23:56
- 1 Respostas
- 5178 Exibições
- Última mensagem por adauto martins

Qui Dez 08, 2016 09:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![z=\frac{x^2+y^2}{\sqrt[]{x+y}} z=\frac{x^2+y^2}{\sqrt[]{x+y}}](/latexrender/pictures/613101109245f528c9bf809a7d5d3079.png) , então
, então 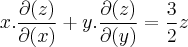 para y>-x
para y>-x
![z=\frac{x^2+y^2}{\sqrt[]{x+y}} z=\frac{x^2+y^2}{\sqrt[]{x+y}}](/latexrender/pictures/613101109245f528c9bf809a7d5d3079.png) , então
, então 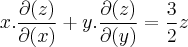 para y>-x
para y>-x
![{z}_{x}=(\partial/\partial x)({x}^{2}+{y}^{2}/\sqrt[]{x+y})=(\sqrt[]{x+y}.(2x)-(1/2)({x}^{2}+{y}^{2}/\sqrt[](x+y)))/(\sqrt[]{x+y})^2 {z}_{x}=(\partial/\partial x)({x}^{2}+{y}^{2}/\sqrt[]{x+y})=(\sqrt[]{x+y}.(2x)-(1/2)({x}^{2}+{y}^{2}/\sqrt[](x+y)))/(\sqrt[]{x+y})^2](/latexrender/pictures/df36a5f8952b1ad4609c6819ac3a8472.png) =
=![=(4x(x+y)-({x}^{2}+{y}^{2}))/2.({\sqrt[]{x+y}})^{3} =(4x(x+y)-({x}^{2}+{y}^{2}))/2.({\sqrt[]{x+y}})^{3}](/latexrender/pictures/490c515a025da4a660c3315a1a138993.png) ...analogamente p/
...analogamente p/![{z}_{y}=(4y(x+y)-({x}^{2}+{y}^{2}))/2.({\sqrt[]{x+y}})^{3} {z}_{y}=(4y(x+y)-({x}^{2}+{y}^{2}))/2.({\sqrt[]{x+y}})^{3}](/latexrender/pictures/5539da7f51097c8e0ba17ef5259d3847.png) ...logo:
...logo:![x{z}_{y}+y{z}_{y}=(4{x}^{2}(x+y)-xz)+(4{y}^{2}(x+y)-yz)/2.({\sqrt[]{x+y}})^{3}[tex] x{z}_{y}+y{z}_{y}=(4{x}^{2}(x+y)-xz)+(4{y}^{2}(x+y)-yz)/2.({\sqrt[]{x+y}})^{3}[tex]](/latexrender/pictures/5915402a310b3c728c5c0288990b5637.png)
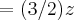



 , avisa que eu resolvo.
, avisa que eu resolvo.

