 por JaderCordoval » Qua Nov 19, 2014 16:19
por JaderCordoval » Qua Nov 19, 2014 16:19
[Exercício de Cálculo - Limites]
Boa tarde, tenho uma professora de cálculo muito ruim, não sabe explicar nada, e dá alguns exercício, muito difíceis de resolver. Fiquei 42 anos sem estudar e voltei agora, estou tendo muita dificuldade na matéria. Preciso de ajuda.
Grato, Jáder
Ola, seguem as questões.
1) Considere o gráfico da figura e responda as questões a seguir:
a) Quais os limites de x tendendo aos valores a, o e b?
b) Existe limite da função quando x tende a menos infinito?
c) Existe limite da função quando x tende a mais infinito?
O que você pode afirmar a respeito dos valores c, d, e, g e h?
- Anexos
-

- [Exercício de Cálculo - Limites]
Editado pela última vez por
JaderCordoval em Sex Nov 21, 2014 08:02, em um total de 1 vez.
-
JaderCordoval
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Nov 19, 2014 15:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de InformaçÃo
- Andamento: cursando
 por adauto martins » Qui Nov 20, 2014 10:47
por adauto martins » Qui Nov 20, 2014 10:47
caro jader,
poste melhor o problema,como esta nao estou conseguindo ler as questoes...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por JaderCordoval » Sex Nov 21, 2014 08:04
por JaderCordoval » Sex Nov 21, 2014 08:04
Bom dia, obrigado por responder.
Segue as questões.
1) Considere o gráfico da figura e responda as questões a seguir:
a) Quais os limites de x tendendo aos valores a, o e b?
b) Existe limite da função quando x tende a menos infinito?
c) Existe limite da função quando x tende a mais infinito?
O que você pode afirmar a respeito dos valores c, d, e, g e h?
Grato, Jáder
-
JaderCordoval
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Nov 19, 2014 15:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de InformaçÃo
- Andamento: cursando
 por adauto martins » Sex Nov 21, 2014 14:12
por adauto martins » Sex Nov 21, 2014 14:12
limites laterais...
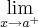
,sao limites de valores aproximando-se de a,pela direita...ou seja por valores maiores q.a(
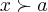
)...
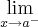
,sao limites de valores aproximando-se pela esquerda de a,ou seja ,valores
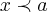
...quando esses valores sao iguais dizemos q. existe o limite em a,e seu valor sera y=f(a) p/ funçoes continuas...dito isso vamos a resoluçao:
a)
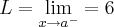
,acho ser 6 mesmo,e a imagem(eixo yy) da bolinha aberta...
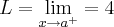
....
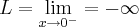
...
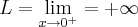
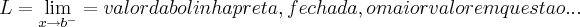
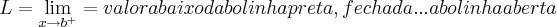
...escrevo assim pq nao consigo enxergar os valores do grafico...em funçao do exposto acima,resolva as outras questoes...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por JaderCordoval » Sáb Nov 22, 2014 11:21
por JaderCordoval » Sáb Nov 22, 2014 11:21
Bom dia Adauto.
Estou te reenviando o gráfico, pra ver se vc consegue vê-lo.
Ele contem somente letras, não tem números.
O problema que aqui, só estou conseguindo anexar arquivos em JPG.
Mas de toda forma agradeço imensamente pela sua ajuda.
Segue abaixo as resposta que não sei se estão corretas, mas pelo menos estou tentando resolver.
ATIVIDADE AVALIATIVA 06
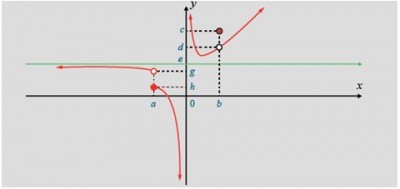
1) Considere o gráfico da figura e responda as questões a seguir:
a) Quais os limites de x tendendo aos valores a, o e b?
lim de a= h
lim de b= c
lim de 0 =
b) Existe limite da função quando x tende a menos infinito?
-?
c) Existe limite da função quando x tende a mais infinito?
+?
O que você pode afirmar a respeito dos valores c, d, e, g e h?
O valor c é o lim de b
O valor h é o lim de a
- Anexos
-
- EXERCÍCIO DE CÁLCULO - LIMITES
-
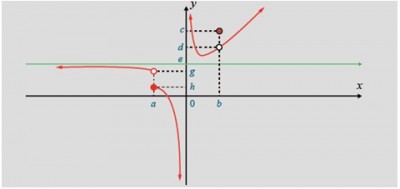
- Gráfico
-
JaderCordoval
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Nov 19, 2014 15:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de InformaçÃo
- Andamento: cursando
 por adauto martins » Sáb Nov 22, 2014 14:23
por adauto martins » Sáb Nov 22, 2014 14:23
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4812 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5569 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] exercicio limites envolvendo ln
por lucasdemirand » Qua Jul 10, 2013 00:31
- 1 Respostas
- 2247 Exibições
- Última mensagem por young_jedi

Qua Jul 10, 2013 21:48
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] exercicio de limites tendendo a zero
por lucasdemirand » Qui Jul 11, 2013 18:00
- 1 Respostas
- 1806 Exibições
- Última mensagem por e8group

Sex Jul 12, 2013 11:43
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Exercício com limites notáveis
por fff » Sáb Fev 08, 2014 21:41
- 3 Respostas
- 2683 Exibições
- Última mensagem por e8group

Dom Fev 09, 2014 15:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



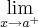 ,sao limites de valores aproximando-se de a,pela direita...ou seja por valores maiores q.a(
,sao limites de valores aproximando-se de a,pela direita...ou seja por valores maiores q.a(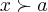 )...
)...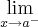 ,sao limites de valores aproximando-se pela esquerda de a,ou seja ,valores
,sao limites de valores aproximando-se pela esquerda de a,ou seja ,valores 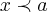 ...quando esses valores sao iguais dizemos q. existe o limite em a,e seu valor sera y=f(a) p/ funçoes continuas...dito isso vamos a resoluçao:
...quando esses valores sao iguais dizemos q. existe o limite em a,e seu valor sera y=f(a) p/ funçoes continuas...dito isso vamos a resoluçao: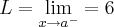 ,acho ser 6 mesmo,e a imagem(eixo yy) da bolinha aberta...
,acho ser 6 mesmo,e a imagem(eixo yy) da bolinha aberta...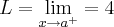 ....
....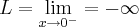 ...
...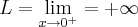
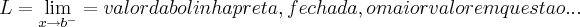
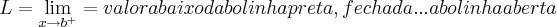 ...escrevo assim pq nao consigo enxergar os valores do grafico...em funçao do exposto acima,resolva as outras questoes...
...escrevo assim pq nao consigo enxergar os valores do grafico...em funçao do exposto acima,resolva as outras questoes...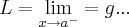
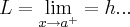
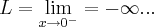
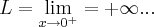
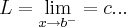
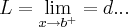
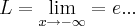
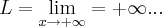
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.