Vencill escreveu: Se F(x)=f(xf(xf(x))) com f(1)=2, f(2)=3, f' (1)=4, f'(2)=5 e f' (3)=6, determinar F' (1).
Olá!
Então, eu estava justamente pensando neste quando vc respondeu. É mais complicado. Mas, eu vou tentar. Na minha primeira tentativa, a resposta deu 120. Estou achando que aqueles "x" que não estão dentro da f, isto é, f(x), que aparece no meio das contas deve ser considerado uma função, a função identidade. Então, fica assim:
Seja x = g (x). Temos: F(x) = f(g(x)f(g(x).f(x))) (preste bastante atenção nos parênteses, ficou um pouco confuso, mas é isso).
Então, F'(x) = (g(x)f(g(x).f(x)))' . f '(g(x)f(g(x).f(x))).
Agora, vamos separar:
(*) = (g(x)f(g(x).f(x)))' = g'(x) . f(g(x).f(x)) + f '(g(x).f(x)) . g(x) = 1 . f(xf(x)) + f '(x.f(x)) . x = f(xf(x)) + xf '(xf(x)). Daí, aplicando em x = 1, temos:
(*) = f(1.f(1)) + 1. f '(1f(1)) = f(2) + f '(2) = 3 + 5 = 8.
(**) = f '(g(x)f(g(x).f(x))) = f '(x(f(xf(x))) = f '(1.f(1.f(1))) = 6.
Bom, acaba que F'(1) = 8 . 6 = 48.
De novo eu não encontrei a resposta certa. Sinto muito. Depois, posso tentar com mais calma. Mas, a ideia é essa. Neste caso, temos muitas composições. E eu não consigo encontrar o meu erro. Desculpe. O que você acha? Tente aplicar essa ideia.



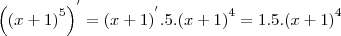
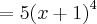 . Daí, seguindo essa ideia, temos:
. Daí, seguindo essa ideia, temos:

