[Integral Dupla] Integral sem solução

por **KleinIll** » Qua Mar 20, 2013 16:32

$\int_{0}^{1}\int_{0}^{1} xy{(x^2 + y^2 + 1)}^{-\frac{1}{2}}dydx$

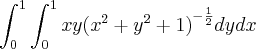
Derivando em y chego à:

$\left{(x^3 + 2x^2)}^{\frac{1}{2}} - {(x^3 + x^2)}^{\frac{1}{2} \right$

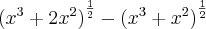
E apartir daí não consigo solução para a integral.

Como faz o cálculo desta integral dupla?

* Por favor, desconsidere o tópico, foi erro de conta e no lugar desta integral parcial em y, encontro a expressão x[(x² + 2)^(1/2) - (x² + 1)^(1/2)]

por **Russman** » Qua Mar 20, 2013 19:10

De onde vem essa expressão?

por **adauto martins** » Dom Out 12, 2014 16:36

$\int_{0}^{1}\int_{0}^{1}(xy)/\sqrt[2]{{x}^{2}+{y}^{2}+1}dxdy$ ,faz.x=rcosx,y=rsenx,teremos: $\int_{0}^{1}\int_{0}^{1}(({r}^{2})(cos\theta)(sen\theta)\sqrt[2]{{rcosx}^{2}+{rsenx}^{2}+1})(-{r}^{2}((cos\theta)(sen\theta))drd\theta$
$\int_{0}^{\pi/2}{-(cos\theta(sen\theta))}^{2}(\int_{0}^{1}({r}^{4}/(\sqrt[2]{{r}^{2}+1})dr)d\theta$ ...na integraçao em relaçao a r,faz-se u= $\sqrt[2]{{r}^{2}+1}$ e na segunda integraçao,em relaçao a $\theta$ ,faz-se v=sen $\theta$ ,levando-se em conta os limites de integraçao(0,1)...ai por substituiçao calcula-se a integral...

[Integral Dupla] Integral sem solução

[Integral Dupla] Integral sem solução

[Integral Dupla] Integral sem solução

Re: [Integral Dupla] Integral sem solução

Re: [Integral Dupla] Integral sem solução

Quem está online