 por marinalcd » Qui Ago 14, 2014 23:07
por marinalcd » Qui Ago 14, 2014 23:07
Estou com dificuldade nessa questão. Podem me ajudar?
Seja A = [0,1)

(
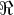
\Q). Podemos dizer que A é um intervalo? Por quê? Inf=? sup=?
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por e8group » Sex Ago 29, 2014 16:37
por e8group » Sex Ago 29, 2014 16:37
Dados a,b reais define-se o intervalo fechado
![[a,b] := \{x \in \mathbb{R} ; a \leq x\leq b \} [a,b] := \{x \in \mathbb{R} ; a \leq x\leq b \}](/latexrender/pictures/04fbc74068dc42567c4798616f7105c6.png)
e o aberto
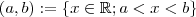
Sobre o exercício verifique-se que supremo do conjunto requerido é 1 e o ínfimo 0 . O segundo passo é mostrar que existe algum x real entre 0 e 1[mais precisamente x racional ] ,(i.e, ele pertence ao intervalo aberto (0,1) ) de modo que tal número não está no conjunto exposto .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11055 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10765 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12532 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3157 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida!!
por GABRIELA » Qui Set 17, 2009 18:19
- 5 Respostas
- 5726 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (
(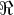 \Q). Podemos dizer que A é um intervalo? Por quê? Inf=? sup=?
\Q). Podemos dizer que A é um intervalo? Por quê? Inf=? sup=?
![[a,b] := \{x \in \mathbb{R} ; a \leq x\leq b \} [a,b] := \{x \in \mathbb{R} ; a \leq x\leq b \}](/latexrender/pictures/04fbc74068dc42567c4798616f7105c6.png) e o aberto
e o aberto 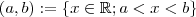



 , avisa que eu resolvo.
, avisa que eu resolvo.

