 por wvyeyra » Ter Jul 22, 2014 21:31
por wvyeyra » Ter Jul 22, 2014 21:31
Olá! Poderiam me ajudar a calcular esse limite trigonométrico?
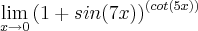
.
A minha lógica é:
* Quando x vai pra zero sin(7x) vai pra zero tbm. Então (1 + sin(7x)) = 1
* E cot(5x) = cos(5x)/sin(5x). Temos que qnd x se aproxima de zero o denominador sin(5x) tende a zero e o numerador cos(5x) tende a 1. Aí temos que o inverso de algo muito pequeno é algo muito grande, ou seja, infinito.
* Daí eu cheguei em algo parecido com 1^(infinito)= infinito.
Observações: sou muito leigo ainda na matéria de cálculo. Então gostaria de uma explicação simples, se possível. E outra, coloquei no site wolframalpha e ele deu o resultado ( e^(7/5)).
Desde já agradeço!
-
wvyeyra
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jul 22, 2014 21:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Ter Jul 22, 2014 22:40
por e8group » Ter Jul 22, 2014 22:40
1^(infinto) é indeterminado .
Minha sugestão ,defina
![L(x) = (1+sin(7x))^{cot(5x)} = \left [(1+sin(7x))^{\frac{1}{sin(5x)} \right]^{cos(5x)} L(x) = (1+sin(7x))^{cot(5x)} = \left [(1+sin(7x))^{\frac{1}{sin(5x)} \right]^{cos(5x)}](/latexrender/pictures/376f0197ef74a57cc8e8d41fecf9ac7d.png)
.
Aplicando o logaritmo natural em ambos membros temos
![ln(L(x)) = cos(5x)\frac{1}{sin(5x)} \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} } = ln(L(x)) = cos(5x)\frac{1}{sin(5x)} \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} } =](/latexrender/pictures/9b575053fa5d3f3623d34028efa7d7e0.png)
![= cos(5x) \cdot \frac{1}{sin(5x)} \cdot sin(7x) \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} = = cos(5x) \cdot \frac{1}{sin(5x)} \cdot sin(7x) \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} =](/latexrender/pictures/643a9e0844183d5ab250272404b6e648.png)
![= \frac{7}{5} \cdot cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}} = \frac{7}{5} \cdot cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}}](/latexrender/pictures/9d0c138afa5a858f69f7471c4a0af7c4.png)
.
Agora está mais fácil ... passando ao limite com x tendendo à zero , temos no segundo membro que ( verifique !)
![\frac{7}{5} \lim_{x \to 0 }cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}} = \frac{7}{5} \frac{7}{5} \lim_{x \to 0 }cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}} = \frac{7}{5}](/latexrender/pictures/b2b066841338be27ea69a7e7de3c723f.png)
.Note também que (devido a continuidade )
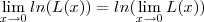
.Desta forma ,temos
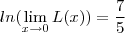
e portanto
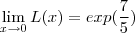
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7267 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] calculo de limite trigonométrico
por PRADO » Dom Mai 22, 2016 17:01
- 2 Respostas
- 5631 Exibições
- Última mensagem por PRADO

Sex Jun 03, 2016 23:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico]
por Ana_Rodrigues » Qui Jan 26, 2012 18:54
- 4 Respostas
- 2861 Exibições
- Última mensagem por Ana_Rodrigues

Sex Jan 27, 2012 14:28
Cálculo: Limites, Derivadas e Integrais
-
- Limite trigonométrico
por jmoura » Dom Mar 25, 2012 21:25
- 2 Respostas
- 2077 Exibições
- Última mensagem por LuizAquino

Seg Mar 26, 2012 13:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
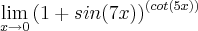 .
.

![L(x) = (1+sin(7x))^{cot(5x)} = \left [(1+sin(7x))^{\frac{1}{sin(5x)} \right]^{cos(5x)} L(x) = (1+sin(7x))^{cot(5x)} = \left [(1+sin(7x))^{\frac{1}{sin(5x)} \right]^{cos(5x)}](/latexrender/pictures/376f0197ef74a57cc8e8d41fecf9ac7d.png) .
. ![ln(L(x)) = cos(5x)\frac{1}{sin(5x)} \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} } = ln(L(x)) = cos(5x)\frac{1}{sin(5x)} \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} } =](/latexrender/pictures/9b575053fa5d3f3623d34028efa7d7e0.png)
![= cos(5x) \cdot \frac{1}{sin(5x)} \cdot sin(7x) \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} = = cos(5x) \cdot \frac{1}{sin(5x)} \cdot sin(7x) \cdot ln \left [1+sin(7x) \right]^{\frac{sin(7x)}{sin(7x)} =](/latexrender/pictures/643a9e0844183d5ab250272404b6e648.png)
![= \frac{7}{5} \cdot cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}} = \frac{7}{5} \cdot cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}}](/latexrender/pictures/9d0c138afa5a858f69f7471c4a0af7c4.png) .
. ![\frac{7}{5} \lim_{x \to 0 }cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}} = \frac{7}{5} \frac{7}{5} \lim_{x \to 0 }cos(5x) \cdot \frac{1}{\dfrac{sin(5x)}{5x} } \cdot \frac{sin(7x)}{7x} \cdot ln \left [1+sin(7x) \right]^{\frac{1}{sin(7x)}} = \frac{7}{5}](/latexrender/pictures/b2b066841338be27ea69a7e7de3c723f.png) .Note também que (devido a continuidade )
.Note também que (devido a continuidade ) 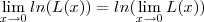 .Desta forma ,temos
.Desta forma ,temos 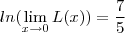 e portanto
e portanto 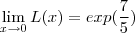



 , avisa que eu resolvo.
, avisa que eu resolvo.

