Questão:
Seja
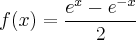 .
. Mostre que f é inversível e determine sua inversa g.
a resposta desta questão é
![y=ln(x+\sqrt[]{x^2+1}) y=ln(x+\sqrt[]{x^2+1})](/latexrender/pictures/6bd04df41e39d5510766e90a09132db9.png) , manipulei algebricamente mas não sei onde errei.
, manipulei algebricamente mas não sei onde errei.
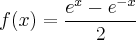 .
. ![y=ln(x+\sqrt[]{x^2+1}) y=ln(x+\sqrt[]{x^2+1})](/latexrender/pictures/6bd04df41e39d5510766e90a09132db9.png) , manipulei algebricamente mas não sei onde errei.
, manipulei algebricamente mas não sei onde errei.
 foi definida de
foi definida de  em
em  .
.  satisfaz um dos itens (a),(b) ou (c) juntamente com (d) ou (e) , então
satisfaz um dos itens (a),(b) ou (c) juntamente com (d) ou (e) , então  é bijetora .(admite inversa)
é bijetora .(admite inversa) 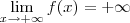 e
e 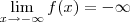 .Como
.Como  é contínua , (pois é escrita como soma de duas funções contínuas ) , então dado qualquer
é contínua , (pois é escrita como soma de duas funções contínuas ) , então dado qualquer 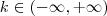 , o TVI garanti que existe
, o TVI garanti que existe  em
em 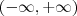 t.q
t.q  o que implica
o que implica  sobrejetiva .
sobrejetiva .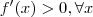 (verifique )[isso significa que f é estritamente crescente ] .
(verifique )[isso significa que f é estritamente crescente ] .  real (a princípio arbitrário , se precisar de + hipóteses , trabalhe em cima dos casos isoladamente) . Note que
real (a princípio arbitrário , se precisar de + hipóteses , trabalhe em cima dos casos isoladamente) . Note que 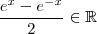 . Deixe
. Deixe 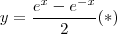 isto equivale
isto equivale 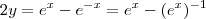 . Agora resolva a eq. para
. Agora resolva a eq. para 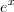 e depois tome o ln em ambos lados . (Dica use a fórmula resolvente e.q segundo grau ) .
e depois tome o ln em ambos lados . (Dica use a fórmula resolvente e.q segundo grau ) . correspondente através de (*) , e reciprocamente ; para cada y que escolho consigo obter um único
correspondente através de (*) , e reciprocamente ; para cada y que escolho consigo obter um único  obtido pela solução acima .
obtido pela solução acima .
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante