 por barbara-rabello » Ter Jun 03, 2014 21:32
por barbara-rabello » Ter Jun 03, 2014 21:32
Bom, estou estudando sistemas de equações diferenciais e acabei de ver a parte com autovalores complexos, onde usamos Euler para resolver.
Esta parte consegui entender. A questão é, aprendi para casos com autovalores imaginários puros, mas como faço quando, ao estudar algum sistema,
encontrar autovalores da forma a + bi? Não consegui achar nenhum exemplo para me ajudar nessa dúvida, tentei pensar sozinha, mas na hora de usar
Euler estou me enrolando e não consigo fazer. Alguém tem algum exemplo de como faço nesses casos?
Obrigada!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Russman » Qui Jun 05, 2014 16:40
por Russman » Qui Jun 05, 2014 16:40
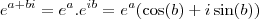
Em geral, é assim que interpreta-se a exponencial complexa.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por barbara-rabello » Sex Jun 06, 2014 19:14
por barbara-rabello » Sex Jun 06, 2014 19:14
Muito obrigada, ajudou bastante!!!!!
Tenho uma outra dúvida: Se tenho um sistema de três equações, por exemplo, então encontro três autovalores e autovetores, respectivamente.
Por exemplo, encontro um autovalor f + gi, e seu respectivo autovetor é
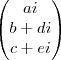
Assim, na hora que calculo Euler ficaria assim:?
![\begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}
+ i
\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}\left[cos(gt)+ isen(gt) \right] \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}
+ i
\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}\left[cos(gt)+ isen(gt) \right]](/latexrender/pictures/ac8f5d03462ba94735ddda40c0817030.png)
Aplicando algumas propriedades algébricas, teríamos:
![\left[ \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.cos(gt)- \begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{1} + \left[\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.cos(gt) + \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{2} \left[ \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.cos(gt)- \begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{1} + \left[\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.cos(gt) + \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{2}](/latexrender/pictures/ebbb561f367ec6243c6b84b379e8e730.png)
Eu tenho que calcular isso para os três autovalores e autovetores e depois somar tudo, ou posso simplesmente calcular somente para um autovalor e, seu respectivo autovetor, para encontrar uma solução geral?
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Autovetores e autovalores em equações quadráticas
por frogman » Dom Dez 10, 2017 15:08
- 0 Respostas
- 1850 Exibições
- Última mensagem por frogman

Dom Dez 10, 2017 15:08
Geometria Analítica
-
- Equações diferenciais
por tiagofabre » Sex Set 21, 2012 00:48
- 1 Respostas
- 1866 Exibições
- Última mensagem por MarceloFantini

Sex Set 21, 2012 01:14
Cálculo: Limites, Derivadas e Integrais
-
- equacoes diferenciais
por Thais Bomfim » Qua Dez 12, 2012 01:58
- 2 Respostas
- 2200 Exibições
- Última mensagem por Thais Bomfim

Qua Dez 12, 2012 14:02
Equações
-
- Equações Diferenciais
por sergio2205 » Qua Mar 06, 2013 13:27
- 1 Respostas
- 1740 Exibições
- Última mensagem por Russman

Qua Mar 06, 2013 15:14
Equações
-
- Equações Diferenciais
por marinalcd » Sex Ago 09, 2013 15:19
- 1 Respostas
- 1640 Exibições
- Última mensagem por Man Utd

Dom Jun 15, 2014 17:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


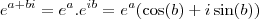

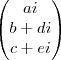
![\begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}
+ i
\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}\left[cos(gt)+ isen(gt) \right] \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}
+ i
\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}\left[cos(gt)+ isen(gt) \right]](/latexrender/pictures/ac8f5d03462ba94735ddda40c0817030.png)
![\left[ \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.cos(gt)- \begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{1} + \left[\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.cos(gt) + \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{2} \left[ \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.cos(gt)- \begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{1} + \left[\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.cos(gt) + \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{2}](/latexrender/pictures/ebbb561f367ec6243c6b84b379e8e730.png)