 por Atom » Dom Mai 25, 2014 20:22
por Atom » Dom Mai 25, 2014 20:22
Como resolve limites quando eles tem duas raízes?
Por exemplo:
lim quando x tende à 0 de f(x), f(x)= [(raíz de x+3) - (raíz de 3)] / x. Resposta: raíz de 2 / 4
ou
lim quando x tende à 1 de f(x), f(x)= [(raíz de x+3) - (2)] / (raíz de x) - (1). Resposta: 1 / 2
Valeu!
-
Atom
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 25, 2014 20:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Mai 25, 2014 21:59
por e8group » Dom Mai 25, 2014 21:59
Por favor ,utilize LaTeX . (Sem impor condições em a e b deixo a vc ) Pense qual a relação entre
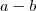
e
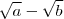
. Você sabe fatorar
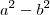
? Se sim também saberá
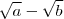
.Dica :
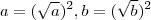
. Então
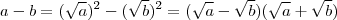
e assim
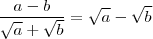
.
Entendeu porque eu disse que se você souber fatorar
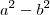
vc tbm consegue para potencias de

inversa . Note que este resultado também é obtido por simplesmente multiplicar pelo conjugado . OK, se tivéssemos diferenças de raiz cubica ,novamente aqui lhe pergunto , vc sabe fatorar
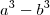
? Se sim , também saberá para
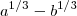
. Mesma dica :

.
E podemos generalizar ....
Se sabemos fatorar

também saberemos
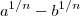
, pois ,
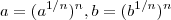
.
Entendeu ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] - LIMITES DE DUAS VARIAVEIS
por Jol » Ter Fev 26, 2013 19:33
- 1 Respostas
- 1986 Exibições
- Última mensagem por young_jedi

Qua Fev 27, 2013 18:43
Cálculo: Limites, Derivadas e Integrais
-
- Limites com duas equações
por Marcelo_td » Seg Jan 03, 2011 01:48
- 1 Respostas
- 1402 Exibições
- Última mensagem por Elcioschin

Seg Jan 03, 2011 12:10
Cálculo: Limites, Derivadas e Integrais
-
- Limites duas variaveis
por Razoli » Qui Jul 03, 2014 23:22
- 2 Respostas
- 2596 Exibições
- Última mensagem por Razoli

Qui Jul 03, 2014 23:41
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Função de duas variáveis
por Sohrab » Ter Abr 23, 2013 03:18
- 7 Respostas
- 6786 Exibições
- Última mensagem por brunno10

Qua Mai 01, 2013 00:28
Cálculo: Limites, Derivadas e Integrais
-
- Limites, conjugado de raizes
por moyses » Qui Out 06, 2011 12:16
- 19 Respostas
- 25775 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 19:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


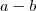 e
e 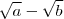 . Você sabe fatorar
. Você sabe fatorar 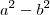 ? Se sim também saberá
? Se sim também saberá 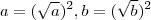 . Então
. Então 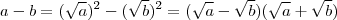 e assim
e assim 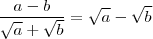 .
.  inversa . Note que este resultado também é obtido por simplesmente multiplicar pelo conjugado . OK, se tivéssemos diferenças de raiz cubica ,novamente aqui lhe pergunto , vc sabe fatorar
inversa . Note que este resultado também é obtido por simplesmente multiplicar pelo conjugado . OK, se tivéssemos diferenças de raiz cubica ,novamente aqui lhe pergunto , vc sabe fatorar 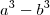 ? Se sim , também saberá para
? Se sim , também saberá para 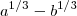 . Mesma dica :
. Mesma dica :  .
.  também saberemos
também saberemos 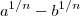 , pois ,
, pois , 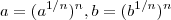 .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.