 por igones » Sex Dez 04, 2009 18:15
por igones » Sex Dez 04, 2009 18:15
Estou estudando derivadas, to indo bem, mas cheguei na parte gráfica e travei nesse exercicio. Não tenho ideia do que fazer pra resolver ele. Ele faz parte de uma apostila que meu professor passou como revisão.
 http://img694.imageshack.us/i/revisao.jpg/
http://img694.imageshack.us/i/revisao.jpg/ (Questão link)
Não entendi como achar tal área.
Obrigado, abraços!
-
igones
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 04, 2009 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por Molina » Sex Dez 04, 2009 20:44
por Molina » Sex Dez 04, 2009 20:44
Boa noite, amigo.
Na verdade essa parte de área seria com Integral.
Já viu este assunto?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por igones » Sex Dez 04, 2009 22:57
por igones » Sex Dez 04, 2009 22:57
Já sim, mas ele acabou de dar integrais essa semana, não estudei muito ainda, só o inicio.
Pode me ajudar se possivel, Abraços!
-
igones
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 04, 2009 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por Molina » Sáb Dez 05, 2009 16:04
por Molina » Sáb Dez 05, 2009 16:04
Bom, vamos lá.
Você entende que integal está relacionada com a área de uma função até o eixo x, correto?
Então vamos dividir esta sua figura em 3 áreas (A1, A2 e A3, nesta ordem) e cálcula-las separadamente. A área total que queremos (em azul) vai ser dado por

.
Vou fazer a primeira área e vamos ver se você pega o macete para as outras:
Se eu quisesse toda a área embaixo da reta
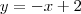
bastava integrar
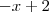
. Porém, perceba que eu quero a área embaixo da reta, porém,
tirando a parte da área da parábola dada por
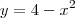
. Note ainda que a área que queremos está entre os pontos -2 e -1. Logo, esses serão os limites da integral:
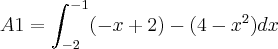
Perceba que o que eu estou fazendo é pegando uma área e
subtraindo pela outra, ficando apenas a área pintada (dentro do intervalo (-2,-1)).
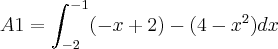
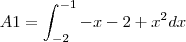
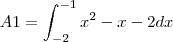
![A1=\left[\frac{x^3}{3}-\frac{x^2}{2}-2x \right]_{-2}^{-1} A1=\left[\frac{x^3}{3}-\frac{x^2}{2}-2x \right]_{-2}^{-1}](/latexrender/pictures/3bb58e6f1e736cd9b2d4b3ba9bebb999.png)
Agora é só substituir os limites da integral no x e descobrir esta área.
Qualquer dúvida comente,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por igones » Sáb Dez 05, 2009 20:12
por igones » Sáb Dez 05, 2009 20:12
Muito obrigado, cosnegui entender.
Mas, não entendi esse intervalo (-2, -1), não to vendo ele na figura =/
Explica essa parte por favor
Obrigado!
Abraços!

-
igones
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 04, 2009 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por Molina » Dom Dez 06, 2009 12:03
por Molina » Dom Dez 06, 2009 12:03
igones escreveu:Muito obrigado, cosnegui entender.
Mas, não entendi esse intervalo (-2, -1), não to vendo ele na figura =/
Explica essa parte por favor
Obrigado!
Abraços!

Bom dia!
O fato de utilizar os limites da integral de -2 a -1 é pq esta figura que queremos calcular a área está entre x = -2 e x = -1. Na segunda figura os limites serão diferentes: (-1 e 2). E na terceira figura será 2 e 3.
Conseguiu ver isso agora?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por igones » Dom Dez 06, 2009 12:36
por igones » Dom Dez 06, 2009 12:36
Consegui sim!
São 3 regioes sombreadas neh?!
Eu só tava vendo 2..
Então vc calculou a área de cada região e depois somou as 3 que da a area total certo?
Obrigado! =D
-
igones
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 04, 2009 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por Molina » Dom Dez 06, 2009 12:58
por Molina » Dom Dez 06, 2009 12:58
igones escreveu:Consegui sim!
São 3 regioes sombreadas neh?!
Eu só tava vendo 2..
Então vc calculou a área de cada região e depois somou as 3 que da a area total certo?
Obrigado! =D
Isso mesmo. Você terá que fazer isso! Soma as três áreas encontradas para obter a área total.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por igones » Dom Dez 06, 2009 21:05
por igones » Dom Dez 06, 2009 21:05
Ei molina, meu professor disse que é pra resolver por derivadas, derivando as equações e achando a área, não entendi direito, mas ele disse que é pra resolver com derivadas.
Iai tem ideia de como fazer por derivadas?
Abraços e obrigado molina
-
igones
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 04, 2009 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por igones » Seg Dez 07, 2009 23:49
por igones » Seg Dez 07, 2009 23:49
O professor pediu pra resolver com derivadas =//
Como faço!?
Abraços!!
-
igones
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 04, 2009 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por Elcioschin » Ter Dez 08, 2009 12:36
por Elcioschin » Ter Dez 08, 2009 12:36
Igones
A derivada NÃO serve para calcular áreas: serve para calcular;
a) Coeficientes angulares de retas tangentes à função em pontos determinados da função.
b) Consequentemente serve para calcular pontos de máximo e mínimo da função, isto é, pontos onde a curva muda de inclinação (neste caso a derivada é nula).
Para cálculo de áreas somente com Cálculo Integral, conforme mostrou muito bem o Molina.
Assim, acredito que o professor tenha explicado mal ou que vc não tenha entendido bem.
Um abraço
Elcio
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por igones » Sex Dez 11, 2009 23:12
por igones » Sex Dez 11, 2009 23:12
Por favor, descupe o incomodo mas eu preciso urgente da resolução dessa questão!
Minha prova é segunda e essa questão vai valer 1,0.
Por favor, se não puderem resolver detalhadamente, só me digam as respostas de A1 A2 e A3 e a Area total!Abraços!!!!

-
igones
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 04, 2009 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em exercicio de derivada 3
por igones » Ter Dez 08, 2009 12:48
- 10 Respostas
- 8956 Exibições
- Última mensagem por igones

Sex Dez 11, 2009 02:02
Cálculo: Limites, Derivadas e Integrais
-
- (Ajuda) Duvida no exercício de derivada.
por Kamila conka » Qui Fev 28, 2013 20:41
- 3 Respostas
- 2156 Exibições
- Última mensagem por Kamila conka

Sex Mar 01, 2013 18:32
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA- Dúvida exercício de otimização
 por gabifzm » Qua Out 23, 2013 16:14
por gabifzm » Qua Out 23, 2013 16:14
- 0 Respostas
- 1464 Exibições
- Última mensagem por gabifzm

Qua Out 23, 2013 16:14
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] TAXA DE VARIAÇÃO - EXERCICIO DUVIDA
por OoluanOo » Dom Mar 03, 2013 18:02
- 1 Respostas
- 2364 Exibições
- Última mensagem por Russman

Dom Mar 03, 2013 19:58
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Dúvida ao calcular uma derivada...
por dileivas » Ter Mai 01, 2012 09:54
- 2 Respostas
- 2266 Exibições
- Última mensagem por dileivas

Ter Mai 01, 2012 17:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 .
.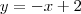 bastava integrar
bastava integrar 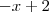 . Porém, perceba que eu quero a área embaixo da reta, porém, tirando a parte da área da parábola dada por
. Porém, perceba que eu quero a área embaixo da reta, porém, tirando a parte da área da parábola dada por 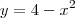 . Note ainda que a área que queremos está entre os pontos -2 e -1. Logo, esses serão os limites da integral:
. Note ainda que a área que queremos está entre os pontos -2 e -1. Logo, esses serão os limites da integral: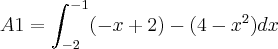
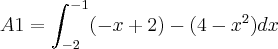
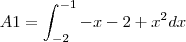
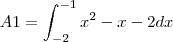
![A1=\left[\frac{x^3}{3}-\frac{x^2}{2}-2x \right]_{-2}^{-1} A1=\left[\frac{x^3}{3}-\frac{x^2}{2}-2x \right]_{-2}^{-1}](/latexrender/pictures/3bb58e6f1e736cd9b2d4b3ba9bebb999.png)














 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?