 por baloso » Sex Abr 25, 2014 19:22
por baloso » Sex Abr 25, 2014 19:22
Olá pessoal, tentei resolver esses limites por conjugados e outras propriedades mas não consegui. Alguém pode me falar quais propriedades eu uso? Mt obg
a)
![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
b)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
c)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)
d) Calcule a,b

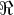
de forma que
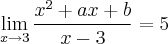
e)
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
f)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
g)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)
-
baloso
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 25, 2014 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Sáb Abr 26, 2014 00:36
por e8group » Sáb Abr 26, 2014 00:36
Boa noite . De acordo com as regras da casa , uma questão por tópico .
Vou te dar uma dica item (d) .
Suponha inicialmente
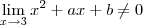
. Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que
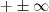
(dependo do sinal do número) .Absurdo ! Logo só podemos ter
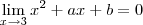
.Logo ,
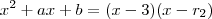
(forma fatorada) [r_2 a segunda raiz do polinômio .
Agora utilizando a forma fatora e a hipótese do limite ser 5 , encontre
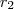
que em consequência obterá as constantes pedidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por baloso » Seg Abr 28, 2014 19:33
por baloso » Seg Abr 28, 2014 19:33
Eu entendi o que você quis dizer. Só olhando deu pra identificar que a raiz é 2.
Então temos que usar
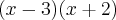
para que a = -1 e b = -6 e lim = 5.
Porém eu não faço a mínima ideia de como provar isso... Eu não posso simplesmente falar que a segunda raiz é 2 e pronto né?
-
baloso
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 25, 2014 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raíz quadrada] Dificuldade com raízes quadradas..
por lucas7 » Ter Ago 30, 2011 21:39
- 5 Respostas
- 3105 Exibições
- Última mensagem por lucas7

Qua Ago 31, 2011 15:18
Conversão de Unidades
-
- Dificuldade com limites e módulos
por Luisags » Qui Abr 12, 2012 23:05
- 5 Respostas
- 3843 Exibições
- Última mensagem por gabriel feron

Ter Abr 17, 2012 03:17
Cálculo: Limites, Derivadas e Integrais
-
- Dificuldade com limites em cálculo I
por Vidotti » Dom Nov 04, 2012 20:42
- 4 Respostas
- 2498 Exibições
- Última mensagem por Vidotti

Dom Nov 04, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limites com duas raízes
por Atom » Dom Mai 25, 2014 20:22
- 1 Respostas
- 2068 Exibições
- Última mensagem por e8group

Dom Mai 25, 2014 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Limites, conjugado de raizes
por moyses » Qui Out 06, 2011 12:16
- 19 Respostas
- 25761 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 19:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)

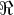 de forma que
de forma que 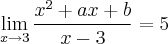
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)

![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)

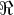 de forma que
de forma que 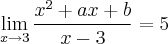
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)

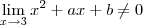 . Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que
. Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que 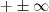 (dependo do sinal do número) .Absurdo ! Logo só podemos ter
(dependo do sinal do número) .Absurdo ! Logo só podemos ter 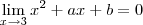 .Logo ,
.Logo , 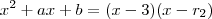 (forma fatorada) [r_2 a segunda raiz do polinômio .
(forma fatorada) [r_2 a segunda raiz do polinômio . 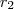 que em consequência obterá as constantes pedidas .
que em consequência obterá as constantes pedidas .
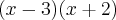 para que a = -1 e b = -6 e lim = 5.
para que a = -1 e b = -6 e lim = 5.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.