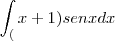 gente achei a seguinte resposta
gente achei a seguinte resposta [tex] sen(x) dx = - cos (x)+ c[\tex]
usando a forma alternativa da integral
[tex]-\frac{1}{2}{e}^{-1x} - \frac{e^1x}{2} +c[\tex]
gostaria de saber se usando essa formula a resposta está correta e se existe outra formula para chegar ao resultado.


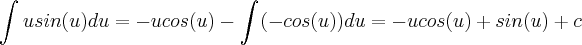 Se voce chamar
Se voce chamar 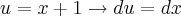 logo
logo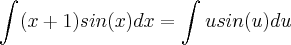 .Por integração por partes
.Por integração por partes 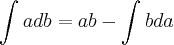 ,irei chamar
,irei chamar 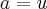 e
e 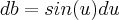 .Como
.Como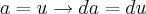 e
e 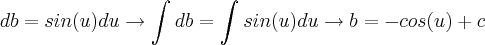 , Logo(irei ignorar a constante).Voltando para a variavel x temos que :
, Logo(irei ignorar a constante).Voltando para a variavel x temos que :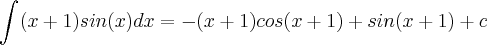

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)