 por thiago15_2 » Qui Fev 27, 2014 01:20
por thiago15_2 » Qui Fev 27, 2014 01:20
Galera, estou com uma duvida grande aqui.
Não tenho prática para escrever as fórmulas mais vai dar pra entender.
A questão é essa:
lim (raizcúbica de 8x-8) + (raizquarta de 16x²+16) -4/(raizquadrada de 4x²+4) -2
x->0
Obs(sem usar derivada)
Meu professor faz a mudança de variável tirando o mmc dos índices. Eu só sei fazer quando dentro da raiz só tem o x. quando tem o x², ou um polinômio, já não sei fazer.
A resposta é 7/6. queria saber mesmo como fica essa mudança de variável.
GRATO.
-
thiago15_2
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Fev 27, 2014 01:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por young_jedi » Sex Fev 28, 2014 15:15
por young_jedi » Sex Fev 28, 2014 15:15
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite com raízes de índices diferentes
por danivelosor » Sáb Mar 28, 2015 21:45
- 0 Respostas
- 1458 Exibições
- Última mensagem por danivelosor

Sáb Mar 28, 2015 21:45
Cálculo: Limites, Derivadas e Integrais
-
- Numero de raízes reais diferentes.
por matheuszila » Dom Nov 28, 2010 14:36
- 6 Respostas
- 3311 Exibições
- Última mensagem por matheuszila

Sex Dez 10, 2010 22:30
Logaritmos
-
- Cálculo com matrizes de tipos diferentes
por Felicia » Ter Set 15, 2009 00:11
- 1 Respostas
- 2049 Exibições
- Última mensagem por Elcioschin

Ter Set 15, 2009 09:19
Matrizes e Determinantes
-
- [índices de Fischer] Estatística
por mngomes » Seg Jul 14, 2008 00:36
- 2 Respostas
- 4137 Exibições
- Última mensagem por Neperiano

Seg Jul 14, 2008 16:24
Estatística
-
- [limite] Dúvida limite com raizes
por rqaugusto » Dom Abr 30, 2017 23:23
- 0 Respostas
- 3115 Exibições
- Última mensagem por rqaugusto

Dom Abr 30, 2017 23:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\lim_{x\to0}\frac{\sqrt[3]{8x+8}+\sqrt[4]{16x^2+16}-4}{\sqrt{4x^2+4}-2} \lim_{x\to0}\frac{\sqrt[3]{8x+8}+\sqrt[4]{16x^2+16}-4}{\sqrt{4x^2+4}-2}](/latexrender/pictures/a6250bb045089b985275d6eddb9ee2fb.png)
![\lim_{x\to0}\frac{2\sqrt[3]{x+1}+2\sqrt[4]{x^2+1}-4}{2\sqrt{x^2+1}-2} \lim_{x\to0}\frac{2\sqrt[3]{x+1}+2\sqrt[4]{x^2+1}-4}{2\sqrt{x^2+1}-2}](/latexrender/pictures/80f275347a1aebb1eea8f0f57a051210.png)
![\lim_{x\to0}\frac{\sqrt[3]{x+1}+\sqrt[4]{x^2+1}-2}{\sqrt{x^2+1}-1} \lim_{x\to0}\frac{\sqrt[3]{x+1}+\sqrt[4]{x^2+1}-2}{\sqrt{x^2+1}-1}](/latexrender/pictures/d71bb1aa07c049484adbb9544e5df62a.png)
![\sqrt[12]{x+1}=y \sqrt[12]{x+1}=y](/latexrender/pictures/1229c27b5acd6a676d155e34ad38a3b0.png)
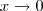
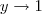
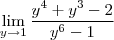
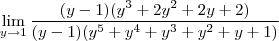
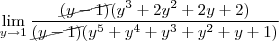
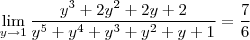


 .
.



