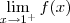 sabendo que, para todo x>1,
sabendo que, para todo x>1, 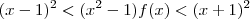

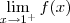 sabendo que, para todo x>1,
sabendo que, para todo x>1, 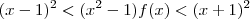

 ,ao dividimos a desigualdade por
,ao dividimos a desigualdade por 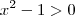 obteremos
obteremos 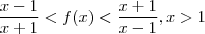 .
. 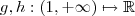 dadas por
dadas por 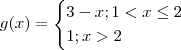 e
e 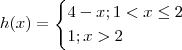
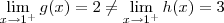 .
.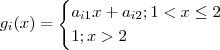 .(a_{ij} ,c constantes fixadas ) [i=0,1,2,...] .Pondo ,
.(a_{ij} ,c constantes fixadas ) [i=0,1,2,...] .Pondo , 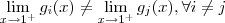 (ambos positivos) e
(ambos positivos) e 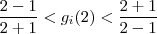 . Impondo que o primeiro o limite seja igual a
. Impondo que o primeiro o limite seja igual a  e para certas escolhas
e para certas escolhas 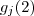 (que condiz com nossa hipótese ) será possível determinar as constantes
(que condiz com nossa hipótese ) será possível determinar as constantes 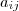 e portanto
e portanto 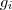 estará bem definido ...
estará bem definido ...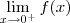 ,exceto se há mais informações sobre
,exceto se há mais informações sobre  e se o enunciado está incorreto .
e se o enunciado está incorreto .
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.