Exercício- D é a região triangular de vértices (0,0), (3,0) e (3,5) e a densidade f em cada ponto
é igual à distância de P ao eixo y.Desenhei a região D, e achei que:
Porém, não consigo encontrar a função f, pois, não entendi essa questão da densidade f em cada ponto ser igual à distância de P ao eixo y.
Se alguém puder ajudar, obrigada.
em ![[0,3]](/latexrender/pictures/ed9c05fe24c0f49f5d73f494a921e0c4.png "[0,3]")
tem-se 
e esta é a propriedade do subconjunt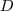o 
do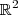 
. Então dado 
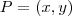em 
será 
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")