 por costav13 » Sáb Nov 09, 2013 10:10
por costav13 » Sáb Nov 09, 2013 10:10
Calcule a derivada das funções dadas utilizando as propriedade
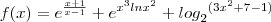
-
costav13
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 28, 2013 11:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sáb Nov 09, 2013 19:15
por e8group » Sáb Nov 09, 2013 19:15
Derive cada termo separadamente .
Considere
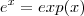
,observe que
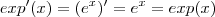
. Então ,
![[exp(h(x))]' = exp(h(x)) \cdot h'(x) [exp(h(x))]' = exp(h(x)) \cdot h'(x)](/latexrender/pictures/c8a895f537c49e39b5ec8924e8a4c569.png)
. Esta fórmula será suficiente p/ determinar a derivada dos dois primeiros termos . Basta então determinar a derivada da função

.
Agora como determinar a derivada de
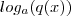
. Onde a é uma constante real positiva e diferente que 1 e
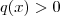
. Considere
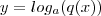
. Por mudança de base ,
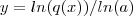
. Derivando-se
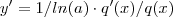
. Agora mudando da base

p/

,obtemos a fórmula
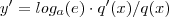
.
Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por costav13 » Sáb Nov 09, 2013 22:33
por costav13 » Sáb Nov 09, 2013 22:33
Não deu pra entender ???
-
costav13
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 28, 2013 11:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Dom Nov 10, 2013 13:29
por e8group » Dom Nov 10, 2013 13:29
Primeira propriedade , "derivada da soma é a soma das derivadas " :
![f'(x) = [exp\left(\frac{x+1}{x-1}\right)]' + [exp\left(x^3ln(x^2) \right)]' + [log_2(3x^2+7 - 1)] ' f'(x) = [exp\left(\frac{x+1}{x-1}\right)]' + [exp\left(x^3ln(x^2) \right)]' + [log_2(3x^2+7 - 1)] '](/latexrender/pictures/6f2fa554eef3faafdee8c97f46fcccbf.png)
.
Agora tome
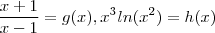
e
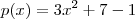
. Temos :
![f'(x) = [exp\left(g(x) \right)]' + [exp\left(h(x) \right)]' + [log_2(p(x))] ' f'(x) = [exp\left(g(x) \right)]' + [exp\left(h(x) \right)]' + [log_2(p(x))] '](/latexrender/pictures/e654d509d59641e928d78fc3ac3207b6.png)
. No post anterior deduzimos fórmulas,vamos aplicar elas ,
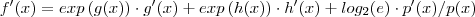
. A resposta final será
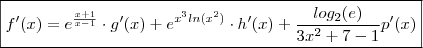
.Agora tente determinar as derivadas das funções
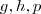
.Comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Não consigo resolver esta questão, por favor me ajudem!
por Derlan » Ter Jul 04, 2017 15:32
- 0 Respostas
- 1956 Exibições
- Última mensagem por Derlan

Ter Jul 04, 2017 15:32
Geometria Analítica
-
- Alguém sabe como resolver????
por DMonteiro » Sáb Abr 03, 2010 23:31
- 4 Respostas
- 3655 Exibições
- Última mensagem por gambit

Ter Fev 17, 2015 00:00
Matemática Financeira
-
- Alguém sabe como resolver???
por DMonteiro » Sáb Abr 03, 2010 23:38
- 4 Respostas
- 3124 Exibições
- Última mensagem por DMonteiro

Dom Abr 04, 2010 21:40
Cálculo: Limites, Derivadas e Integrais
-
- [Equaçoes] alguem que sabe me ajude a resolver.
por teilom » Dom Ago 04, 2013 17:00
- 1 Respostas
- 1485 Exibições
- Última mensagem por DanielFerreira

Dom Ago 04, 2013 20:03
Equações
-
- [Limite] alguem sabe resolver essa expressão?
por tainaraabp » Ter Out 02, 2012 11:35
- 1 Respostas
- 2063 Exibições
- Última mensagem por LuizAquino

Ter Out 02, 2012 12:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
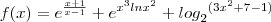


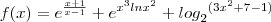

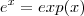 ,observe que
,observe que 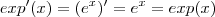 . Então ,
. Então , ![[exp(h(x))]' = exp(h(x)) \cdot h'(x) [exp(h(x))]' = exp(h(x)) \cdot h'(x)](/latexrender/pictures/c8a895f537c49e39b5ec8924e8a4c569.png) . Esta fórmula será suficiente p/ determinar a derivada dos dois primeiros termos . Basta então determinar a derivada da função
. Esta fórmula será suficiente p/ determinar a derivada dos dois primeiros termos . Basta então determinar a derivada da função  .
. 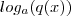 . Onde a é uma constante real positiva e diferente que 1 e
. Onde a é uma constante real positiva e diferente que 1 e 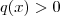 . Considere
. Considere 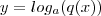 . Por mudança de base ,
. Por mudança de base , 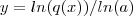 . Derivando-se
. Derivando-se 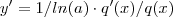 . Agora mudando da base
. Agora mudando da base  p/
p/  ,obtemos a fórmula
,obtemos a fórmula 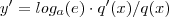 .
.

![f'(x) = [exp\left(\frac{x+1}{x-1}\right)]' + [exp\left(x^3ln(x^2) \right)]' + [log_2(3x^2+7 - 1)] ' f'(x) = [exp\left(\frac{x+1}{x-1}\right)]' + [exp\left(x^3ln(x^2) \right)]' + [log_2(3x^2+7 - 1)] '](/latexrender/pictures/6f2fa554eef3faafdee8c97f46fcccbf.png) .
. 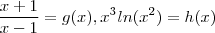 e
e 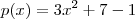 . Temos :
. Temos : ![f'(x) = [exp\left(g(x) \right)]' + [exp\left(h(x) \right)]' + [log_2(p(x))] ' f'(x) = [exp\left(g(x) \right)]' + [exp\left(h(x) \right)]' + [log_2(p(x))] '](/latexrender/pictures/e654d509d59641e928d78fc3ac3207b6.png) . No post anterior deduzimos fórmulas,vamos aplicar elas ,
. No post anterior deduzimos fórmulas,vamos aplicar elas , 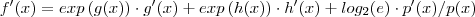 . A resposta final será
. A resposta final será 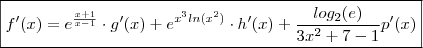 .Agora tente determinar as derivadas das funções
.Agora tente determinar as derivadas das funções 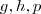 .Comente as dúvidas .
.Comente as dúvidas .

 .
.
 :
: