Seja W(s, t)=F(u(s, t), v(s, t)), onde F, u e v são diferenciáveis e

Encontre
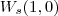 e
e 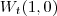 .
.Comentário: Por ser um exercício par não tem a resposta ao final do livro, então gostaria de confirmar com outros membros do fórum. As respostas que encontrei foram:
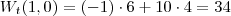 e
e 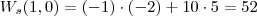 .
.Relembrando a teoria:
1) Notação para Derivadas Parciais:
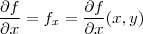
2) Regrada da Cadeia ("Teorema das Funções Implícitas") - duas variáveis:
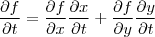
Obrigado!


 .
.
 :
: