Esse problema é mais de cálculo numérico que de cálculo I, mas aí vai.
Como f(x) é um polinômio está mais do que cara que ele é contínuo para todos os reais.
Bem, agora o que você deve fazer é derivar f(x).
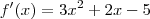
Com isso você encontra os pontos onde f(x) cresce ou decresce e fica mais fácil de você saber onde procurar os valores para o tvi.
Deste modo verificamos que
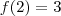
,
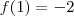
,

,
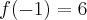
,
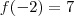
,
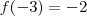
,
Neste casos nós teremos raízes desse polinômio entre [2,1], [1,0],[-3,-2].
Não sei se ficou muito claro para você como eu fiz, mas pense que como a função é contínua, se eu tenho um valor positivo para f(a) e um valor negativo para f(b) , a reta tem de passar por f(x)=0, não tem como ela dar saltos. Este teorema não é perfeito visto que ele me diz que entre [0,2] não tem raíz apesar de eu já ter dito que tem duas raízes neste intervalo, portanto também temos de verificar as derivadas para termos certeza se estamos fazendo direito. Para isso temos que verificar que a função é estritamente crescente ou decrescente neste intervalo, ou seja, verificar se a derivada muda de sinal ou não e claro a derivada tem de ser diferente de zero.



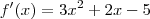
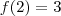 ,
, 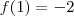 ,
,  ,
, 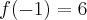 ,
,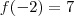 ,
,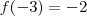 ,
, 


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.