 por Nicolas1Lane » Qui Set 26, 2013 07:56
por Nicolas1Lane » Qui Set 26, 2013 07:56
Dada a seguinte proposição
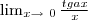
queria saber se minha resolução apresentada abaixo matematicamente descrita é aceitável ou ainda se poderia ser melhorada ou mesmo no caso da existência, me digam dicas para melhorar ainda mais neste aprendizado...
Estou sendo meio redundante, mas isso se deve a enfatização de minha professora de querer que todas as propriedades e etapas de resoluções usadas nos cálculos sejam explicitadas até que se chegue ao produto final.
Assim:
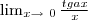
=
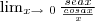
=
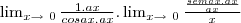
=
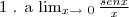
=
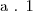
=

-
Nicolas1Lane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Set 11, 2013 23:25
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Exatas/Ciência da Computação
- Andamento: cursando
 por young_jedi » Qui Set 26, 2013 14:08
por young_jedi » Qui Set 26, 2013 14:08
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite - usando apenas limites notáveis
por emsbp » Seg Jul 23, 2012 16:45
- 2 Respostas
- 1986 Exibições
- Última mensagem por emsbp

Ter Jul 24, 2012 16:50
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limites notáveis -->compreender a propriedade usada
por Nicolas1Lane » Qua Set 25, 2013 20:11
- 2 Respostas
- 1805 Exibições
- Última mensagem por Nicolas1Lane

Qua Set 25, 2013 20:45
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Resolução de questão
por malumayara » Qua Set 12, 2012 15:10
- 3 Respostas
- 1935 Exibições
- Última mensagem por MarceloFantini

Qua Set 12, 2012 19:15
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Exercício com limites notáveis
por fff » Sáb Fev 08, 2014 21:41
- 3 Respostas
- 2683 Exibições
- Última mensagem por e8group

Dom Fev 09, 2014 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calcular 2 limites notáveis
por fff » Sex Abr 11, 2014 14:26
- 4 Respostas
- 2530 Exibições
- Última mensagem por fff

Sex Abr 11, 2014 19:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
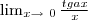 queria saber se minha resolução apresentada abaixo matematicamente descrita é aceitável ou ainda se poderia ser melhorada ou mesmo no caso da existência, me digam dicas para melhorar ainda mais neste aprendizado...
queria saber se minha resolução apresentada abaixo matematicamente descrita é aceitável ou ainda se poderia ser melhorada ou mesmo no caso da existência, me digam dicas para melhorar ainda mais neste aprendizado...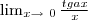
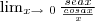
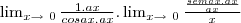
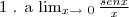
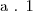



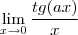
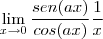
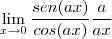
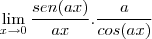
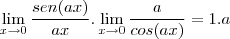



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.