 por Monica santos » Sex Ago 16, 2013 14:22
por Monica santos » Sex Ago 16, 2013 14:22
[tex]\lim_{0}\sqrt[]{a^2+bt-a} (a>0)
t
Vamos lá o professor mandou calcular o limite, porém eu não entendir pelos exemplos que ele me passou e queria algo mais detalhado. Tem outros exemplos que necessito utilizar produtos notaveis, fatoração e mmc . Me ajude por favor .
Me explica isso melhor.
-
Monica santos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Ago 16, 2013 13:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Quimica
- Andamento: cursando
 por young_jedi » Sex Ago 16, 2013 16:15
por young_jedi » Sex Ago 16, 2013 16:15
Não compreendi muito bem este limite seria assim
![\lim_{a\to0}\sqrt[]{a^2+bt-a} \lim_{a\to0}\sqrt[]{a^2+bt-a}](/latexrender/pictures/54a07917a9985edee72769375a9fc6f9.png)
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Monica santos » Sex Ago 16, 2013 16:31
por Monica santos » Sex Ago 16, 2013 16:31
È caso de limite inderteminada .
-
Monica santos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Ago 16, 2013 13:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Quimica
- Andamento: cursando
 por Monica santos » Sex Ago 16, 2013 16:33
por Monica santos » Sex Ago 16, 2013 16:33
correto esse sim, porem é sobre (T) pois não foi junto com a equação
-
Monica santos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Ago 16, 2013 13:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Quimica
- Andamento: cursando
 por young_jedi » Sex Ago 16, 2013 19:01
por young_jedi » Sex Ago 16, 2013 19:01
imagino então que seja isto
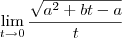
se o a for maior que 1 então temos que
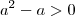
portanto quando t tende a 0 ficamos com uma raiz de
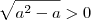
mais isto esta sobre t portanto quando t tende a zero isto tende a infinito

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Como resolver raiz dentro de raiz ?
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
- 10 Respostas
- 13806 Exibições
- Última mensagem por LuizAquino

Sex Ago 24, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
-
- Limite para resolver com raíz no numerador e denominador
por jmoura » Sex Mar 23, 2012 23:20
- 2 Respostas
- 9044 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 24, 2012 08:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas com Raiz e até quando derivar?
por thierryvdb » Ter Jun 01, 2010 09:30
- 2 Respostas
- 21363 Exibições
- Última mensagem por MarceloFantini

Ter Jun 08, 2010 19:08
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2246 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- Limite com raiz enésima - como calcular?
por Brunorp » Ter Mar 24, 2015 08:56
- 1 Respostas
- 8822 Exibições
- Última mensagem por adauto martins

Qui Mar 26, 2015 16:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\lim_{a\to0}\sqrt[]{a^2+bt-a} \lim_{a\to0}\sqrt[]{a^2+bt-a}](/latexrender/pictures/54a07917a9985edee72769375a9fc6f9.png)

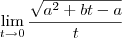
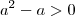
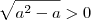


 .
.



