considere a função real de variável real w'(w)=x.lnx
Determine w(x) sabendo que w(1)=0
Alguem me saberá ajudar nesta questão?



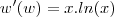
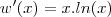


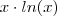 .Neste caso é fácil determinar tal função . Comece observando que a função
.Neste caso é fácil determinar tal função . Comece observando que a função 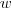 é dada por
é dada por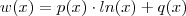 onde
onde 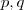 são polinômios . Derivando então
são polinômios . Derivando então 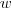 em ordem a
em ordem a  , obtemos :
, obtemos : ![w'(x) = [p(x)\cdot ln(x) + q(x)]' = p'(x) \cdot ln(x) + \frac{p(x)}{x} + q'(x) = x \cdot ln(x) w'(x) = [p(x)\cdot ln(x) + q(x)]' = p'(x) \cdot ln(x) + \frac{p(x)}{x} + q'(x) = x \cdot ln(x)](/latexrender/pictures/54017cc431f24f051634d6daf0b0033f.png) . Comparando a igualdade ,só podemos ter ,
. Comparando a igualdade ,só podemos ter , 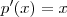 e
e 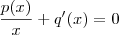 .Assim , fica fácil ver que
.Assim , fica fácil ver que 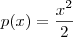 (Por quê ? ) e portanto ,
(Por quê ? ) e portanto , 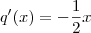 ;donde segue
;donde segue 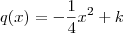 onde
onde  é uma constante (pois,
é uma constante (pois,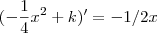 ) . Assim, a função
) . Assim, a função 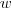 é definida por :
é definida por : 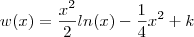 . Agora basta usar que
. Agora basta usar que 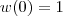 para determinar k .
para determinar k .
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)