 por VenomForm » Qua Jun 19, 2013 13:57
por VenomForm » Qua Jun 19, 2013 13:57
Editado pela última vez por
VenomForm em Qui Jun 20, 2013 11:54, em um total de 1 vez.
-
VenomForm
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Fev 27, 2013 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciências da Computação
- Andamento: cursando
 por VenomForm » Qui Jun 20, 2013 11:54
por VenomForm » Qui Jun 20, 2013 11:54
Dando 1 UP e corrigindo o resultado final
-
VenomForm
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Fev 27, 2013 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciências da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx \int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx](/latexrender/pictures/59f152fc1330f669c380211f223790d3.png)
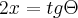
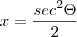
![\frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta \frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta](/latexrender/pictures/9b5cc58a7209758b9e525763e18999c2.png)
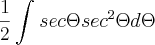
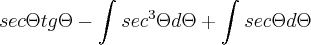
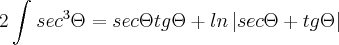
![\int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right] \int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right]](/latexrender/pictures/dd667609adb1cb1b7f3dc6d5fe9ef3bd.png)
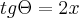
![sec\Theta=\sqrt[2]{1+4{x}^{2}} sec\Theta=\sqrt[2]{1+4{x}^{2}}](/latexrender/pictures/80e79e3b50f340d824c9ca4a616c6d81.png)
![\frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right] \frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right]](/latexrender/pictures/4786cbd03da47f7c1b7f149457c66c07.png)

![\int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx \int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx](/latexrender/pictures/59f152fc1330f669c380211f223790d3.png)
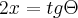
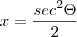
![\frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta \frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta](/latexrender/pictures/9b5cc58a7209758b9e525763e18999c2.png)
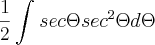
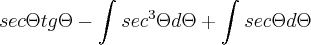
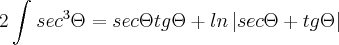
![\int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right] \int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right]](/latexrender/pictures/dd667609adb1cb1b7f3dc6d5fe9ef3bd.png)
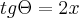
![sec\Theta=\sqrt[2]{1+4{x}^{2}} sec\Theta=\sqrt[2]{1+4{x}^{2}}](/latexrender/pictures/80e79e3b50f340d824c9ca4a616c6d81.png)
![\frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right] \frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right]](/latexrender/pictures/4786cbd03da47f7c1b7f149457c66c07.png)




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.