Determine a área do triângulo formado pelo eixo-x e pelas retas tangentes ao círculo
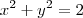nos pontos de interseção do círculo com a parábola de equação 
.
por arthurvct » Qui Jun 13, 2013 15:21
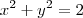nos pontos de interseção do círculo com a parábola de equação .por e8group » Sex Jun 14, 2013 00:49
.Podemos derivar implicitamente também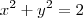 
com respeito a x, mas lembre-se que 
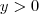.Agora para determinar a interseção , basta substituir 
por 
na equação da circunferência,com isso você determina tais pontos. Supondo que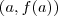 
é um dos pontos ,temos que : 
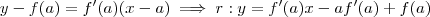.Observando os dois pontos de interseção diferem apenas pela abscissa ,elas são simétricas.Então ,as duas retas diferem apenas pelo coeficiente angular que são iguais em módulo (Verifique !) . Assim , as áreas dos dois retângulos são iguais , e portanto 
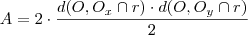é a área que estamos procurando .Agora tente concluir
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)