 por guisaulo » Sáb Jun 08, 2013 14:48
por guisaulo » Sáb Jun 08, 2013 14:48
Considere as retas reversas r e s de equações
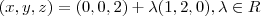
e
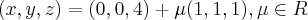
respectivamente. Determine

e
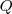
, com
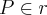
e
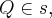
de modo que a distância de P e Q seja a menor possível.
Bem, essa questão esta na seção de máximos e mínimos do meu livro de cálculo de varias variaveis em que estudo. Embora tenha resposta abaixo, eu não consigo entender em como ele obteu a resposta, se alguem puder ajudar...
Resposta:
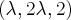
e
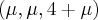
são pontos arbitrários de

e

, respectivamente:
![\sqrt[]{{(\lambda-\mu)}^{2}+{(2\lambda-\mu)}^{2}+{(2+\mu)}^{2}} \sqrt[]{{(\lambda-\mu)}^{2}+{(2\lambda-\mu)}^{2}+{(2+\mu)}^{2}}](/latexrender/pictures/75a00b818e697cba16ee371ed6f8931f.png)
é a distância entre eles.
Basta, então, determinar
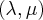
que minimiza
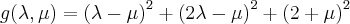
.
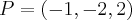
e
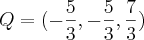
-
guisaulo
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Nov 27, 2012 21:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por young_jedi » Sáb Jun 08, 2013 15:51
por young_jedi » Sáb Jun 08, 2013 15:51
ele calculou as derivadas parciais da função g com relação a lambda e a u e igualou a 0 obtendo duas equação de duas variáveis
com isso ele montou um sistema e encontrou os valores da variáveis
comente se tiver duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por guisaulo » Sáb Jun 08, 2013 16:48
por guisaulo » Sáb Jun 08, 2013 16:48
obrigado @young_jedi consegui resolver a questão
-
guisaulo
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Nov 27, 2012 21:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual a distância entre as duas retas?
por welton » Qui Out 23, 2014 14:46
- 1 Respostas
- 4822 Exibições
- Última mensagem por DanielFerreira

Dom Jan 04, 2015 14:16
Geometria Analítica
-
- G.A. - CÁLCULO DE DISTÂNCIA ENTRE RETAS
por Loretto » Sáb Out 02, 2010 22:19
- 0 Respostas
- 1886 Exibições
- Última mensagem por Loretto

Sáb Out 02, 2010 22:19
Geometria Analítica
-
- Ângulo entre duas retas
por Jonatan » Qui Jul 22, 2010 13:38
- 0 Respostas
- 3589 Exibições
- Última mensagem por Jonatan

Qui Jul 22, 2010 13:38
Geometria Analítica
-
- enconto entre duas retas
por matematicada » Qua Nov 24, 2010 12:14
- 2 Respostas
- 1790 Exibições
- Última mensagem por alexandre32100

Qua Nov 24, 2010 12:59
Funções
-
- Angulo Entre Duas Retas
por mayconf » Sex Set 21, 2012 13:33
- 2 Respostas
- 17743 Exibições
- Última mensagem por mayconf

Sex Set 21, 2012 18:09
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
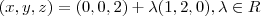
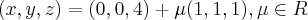
 e
e 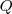 , com
, com 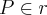 e
e 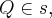 de modo que a distância de P e Q seja a menor possível.
de modo que a distância de P e Q seja a menor possível.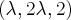 e
e 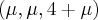 são pontos arbitrários de
são pontos arbitrários de  e
e  , respectivamente:
, respectivamente:![\sqrt[]{{(\lambda-\mu)}^{2}+{(2\lambda-\mu)}^{2}+{(2+\mu)}^{2}} \sqrt[]{{(\lambda-\mu)}^{2}+{(2\lambda-\mu)}^{2}+{(2+\mu)}^{2}}](/latexrender/pictures/75a00b818e697cba16ee371ed6f8931f.png) é a distância entre eles.
é a distância entre eles. 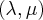 que minimiza
que minimiza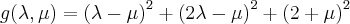 .
.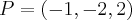 e
e 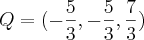



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
