Obrigada desde já!!
por ericaguedes_ » Sex Jun 07, 2013 23:58
por e8group » Sáb Jun 08, 2013 12:40
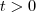suficiente pequeno de modo que a diferença 
e o acréscimo de 
em 
se aproxima cada vez mais de .Suponha que a função 
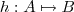esteja definida em e 
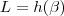.Se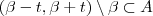 
parece razoável dizer que para quaisquer números 
em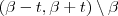 
sempre 
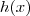se aproxima de 
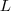já que 
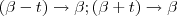,mas isto não necessariamente acontece ,é o caso das funções descontínuas em .
.Vamos aplicar o raciocínio (i) em seu exercício .Como ![D_f =[-3,3]](/latexrender/pictures/94c49f5ccf37caed6252934a0b3cb415.png "D_f =[-3,3]")
basta impor que quando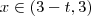 
,tem-se sempre 
,ou seja ,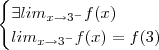
.Desta forma você obterá 
que satisfaça a continuidade da função no ponto 3 .Analogamente ,você achará 
que satisfaça a continuidade de 
no ponto -3 ,basta impor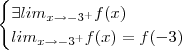 
. 
Voltar para Cálculo: Limites, Derivadas e Integrais
por umbrorz » Dom Abr 15, 2012 00:54
por joaofonseca » Sáb Dez 03, 2011 19:40
por brunotorres123-abc » Sáb Mar 21, 2015 19:35
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo . O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.