 por marcosmuscul » Seg Abr 01, 2013 20:22
por marcosmuscul » Seg Abr 01, 2013 20:22

fiz assim:
![g\prime (x) = 2\left[f\left(cos(x) \right) \right] . \left[f\prime \left(cos(x) \right)\right] \Rightarrow\Rightarrow\Rightarrow g\prime (\frac{\pi}{2}) = 2 . \left[ 1 \right] . \left[ \frac{-1}{2} \right] = -1 g\prime (x) = 2\left[f\left(cos(x) \right) \right] . \left[f\prime \left(cos(x) \right)\right] \Rightarrow\Rightarrow\Rightarrow g\prime (\frac{\pi}{2}) = 2 . \left[ 1 \right] . \left[ \frac{-1}{2} \right] = -1](/latexrender/pictures/e8782715078967834b98b818ae168ae0.png)
Não sei onde está o erro.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por marcosmuscul » Seg Abr 01, 2013 21:07
por marcosmuscul » Seg Abr 01, 2013 21:07
já identifiquei o erro galera.
faltou calcular a derivada de cos(x)
valeu.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Seg Abr 01, 2013 21:12
por e8group » Seg Abr 01, 2013 21:12
Por favor, anexe imagens para o que for estritamente necessário,neste caso não o é ,basta digitar o enunciado completo .Infelizmente não conseguir visuaizar o que era preciso para identificar o seu erro ;mas acredito que temos
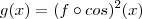
,nestas condições :
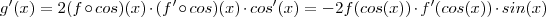
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Me ajudem nesse exercicio!
por Catalao » Qui Nov 01, 2012 20:16
- 1 Respostas
- 1476 Exibições
- Última mensagem por MarceloFantini

Qui Nov 01, 2012 22:59
Geometria Analítica
-
- Me ajudem nesse exercício pfvr!
por andrebessas » Dom Jun 16, 2013 16:45
- 0 Respostas
- 3434 Exibições
- Última mensagem por andrebessas

Dom Jun 16, 2013 16:45
Funções
-
- Ajudem nesse exercício de análise combinatória?
por flor_de_lotus1 » Seg Jun 18, 2012 20:09
- 2 Respostas
- 2226 Exibições
- Última mensagem por fraol

Sáb Ago 11, 2012 15:47
Estatística
-
- [Regra de L'Hôpital]me ajudem nesse exercício.
por marcosmuscul » Sáb Abr 13, 2013 14:07
- 1 Respostas
- 1516 Exibições
- Última mensagem por e8group

Sáb Abr 13, 2013 14:41
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] me ajudem nesse exercicio que eu não entendo
por amanda s » Sáb Nov 16, 2013 17:20
- 1 Respostas
- 1319 Exibições
- Última mensagem por Pessoa Estranha

Sáb Nov 16, 2013 21:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![g\prime (x) = 2\left[f\left(cos(x) \right) \right] . \left[f\prime \left(cos(x) \right)\right] \Rightarrow\Rightarrow\Rightarrow g\prime (\frac{\pi}{2}) = 2 . \left[ 1 \right] . \left[ \frac{-1}{2} \right] = -1 g\prime (x) = 2\left[f\left(cos(x) \right) \right] . \left[f\prime \left(cos(x) \right)\right] \Rightarrow\Rightarrow\Rightarrow g\prime (\frac{\pi}{2}) = 2 . \left[ 1 \right] . \left[ \frac{-1}{2} \right] = -1](/latexrender/pictures/e8782715078967834b98b818ae168ae0.png)


![g\prime (x) = 2\left[f\left(cos(x) \right) \right] . \left[f\prime \left(cos(x) \right)\right] \Rightarrow\Rightarrow\Rightarrow g\prime (\frac{\pi}{2}) = 2 . \left[ 1 \right] . \left[ \frac{-1}{2} \right] = -1 g\prime (x) = 2\left[f\left(cos(x) \right) \right] . \left[f\prime \left(cos(x) \right)\right] \Rightarrow\Rightarrow\Rightarrow g\prime (\frac{\pi}{2}) = 2 . \left[ 1 \right] . \left[ \frac{-1}{2} \right] = -1](/latexrender/pictures/e8782715078967834b98b818ae168ae0.png)


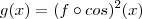 ,nestas condições :
,nestas condições : 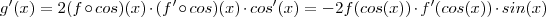 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)