Resolvi a derivada parcial, em relação a x, abaixo e o meu valor não bate com o do livro.
Segue a resolução e a resposta do livro.
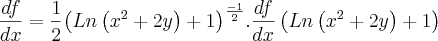
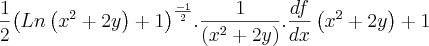
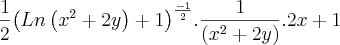
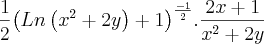
![f(x,y)=\sqrt[]{Ln\left({x}^{2}+2y \right)+1}](/latexrender/pictures/f2cd273ffe59f3ef6a7b79b90f675b4e.png "f(x,y)=\sqrt[]{Ln\left({x}^{2}+2y \right)+1}")
![\frac{x+1}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}](/latexrender/pictures/9bb2999f479756596b425b34a1b91fcd.png "\frac{x+1}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}")
O livro apresenta como resposta:
![\frac{x}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}](/latexrender/pictures/36662203596d5bccdfec5e70cc864d1b.png "\frac{x}{\sqrt[]{Ln\left({x}^{2}+2y \right)+1}.\left({x}^{2}+2y \right)}")
O que eu reparei foi que o livro derivou este "+1", mas eu não entendo o seguinte, se este termo não está dentro dos parenteses porque devo deriva-lo também?
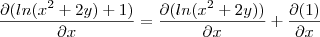
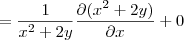
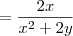
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)