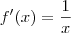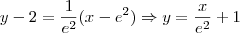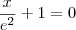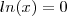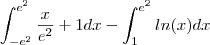por Jhonata » Ter Fev 26, 2013 12:47
por Jhonata » Ter Fev 26, 2013 12:47
Olá, bom dia pessoal.
Estou com um problema na seguinte questão:
Considere a função
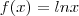
1. Ache a equação da reta tangente ao gráfico de
f(x) quando

;
2. Calcule a área da região limitada por
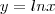
, a reta tangente encontrada no item anterior e o eixo
x.
------
O item 1 eu resolvi facilmente, pois a definição da reta tangente é
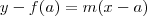
, onde
m é a inclinação da reta tangente (derivada da função).
E quando
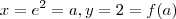
a derivada de f é
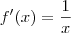
Então a reta tangente é
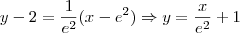
O problema é calcular a área... Não consigo nem imaginar como e onde a curva, a reta e o eixo x se interceptam... Se fosse só a reta e a curva, acho que seria mais fácil... De qualquer forma, quais seriam o intervalos de integração? Se alguém conseguir uma resolução detalhada, eu agradeço.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo 1] reta tangente
por caiofisico » Ter Set 27, 2011 18:38
- 4 Respostas
- 1813 Exibições
- Última mensagem por caiofisico

Ter Set 27, 2011 22:02
Cálculo: Limites, Derivadas e Integrais
-
- [CALCULO] reta tangente
por beel » Ter Out 04, 2011 22:30
- 4 Respostas
- 1663 Exibições
- Última mensagem por beel

Dom Out 09, 2011 13:57
Cálculo: Limites, Derivadas e Integrais
-
- A reta tangente ao gráfico da função (derivadas)
por Ana Maria da Silva » Dom Jun 09, 2013 21:43
- 2 Respostas
- 2077 Exibições
- Última mensagem por Ana Maria da Silva

Qua Jun 12, 2013 20:27
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8672 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- [Reta Paralela à Reta Tangente]
por raimundoocjr » Qui Mai 30, 2013 18:44
- 0 Respostas
- 1156 Exibições
- Última mensagem por raimundoocjr

Qui Mai 30, 2013 18:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
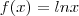
 ;
;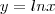 , a reta tangente encontrada no item anterior e o eixo x.
, a reta tangente encontrada no item anterior e o eixo x.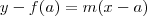 , onde m é a inclinação da reta tangente (derivada da função).
, onde m é a inclinação da reta tangente (derivada da função).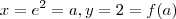 a derivada de f é
a derivada de f é