 por VenomForm » Qua Fev 27, 2013 15:09
por VenomForm » Qua Fev 27, 2013 15:09
-
VenomForm
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Fev 27, 2013 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciências da Computação
- Andamento: cursando
 por young_jedi » Qua Fev 27, 2013 18:54
por young_jedi » Qua Fev 27, 2013 18:54
o metodo esta certo so que os pontos que elas se encontram não

como elas se nos pontos onde

entaõ



ou seja

corrija os limites e refaça as integrais, o resto ta certo
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Qua Fev 27, 2013 19:14
por Russman » Qua Fev 27, 2013 19:14
Você está no caminho certo, apenas vamos organizar as ideias.
As funções que você tem são

e

. A 2° função é a Função Constante que não há nenhum detalhe a se preocupar. Já a 1° função temos um módulo envolvido, de forma que teremos de definí-la por partes. Lembre-se que

de modo que podemos estender esse conceito para um função qualquer

tomando

e resolvendo as equações
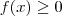
e
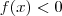
.
No nosso caso temos

cuja solução é
![\left | x^2-4 \right |=\left\{\begin{matrix}
x^2-4 &,-2 \geq x\geq 2 \\
-x^2 + 4 &, 2> x > -2
\end{matrix}\right. = \left\{\begin{matrix}
x^2-4 &,(-\infty ,-2]\cup [2,\infty ) \\
-x^2 + 4 &, (-2,2)
\end{matrix}\right. \left | x^2-4 \right |=\left\{\begin{matrix}
x^2-4 &,-2 \geq x\geq 2 \\
-x^2 + 4 &, 2> x > -2
\end{matrix}\right. = \left\{\begin{matrix}
x^2-4 &,(-\infty ,-2]\cup [2,\infty ) \\
-x^2 + 4 &, (-2,2)
\end{matrix}\right.](/latexrender/pictures/df9731e660f2591b52871cfe9eed3904.png)
Assim, o gráfico das funções é
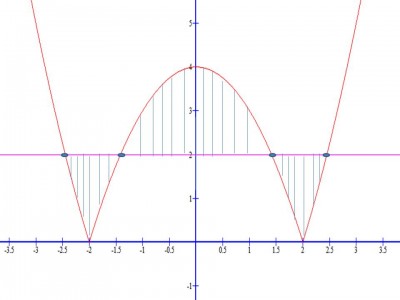
- Gráfico
onde as intersecções estão marcadas com as elipses azuis e a área compreendida entre as funções hachurada.
Temos de determinar os pontos de intersecção. Para isto basta fazer

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área de Região plana limitada por funções
 por iarapassos » Qui Jan 03, 2013 18:52
por iarapassos » Qui Jan 03, 2013 18:52
- 1 Respostas
- 2672 Exibições
- Última mensagem por Russman

Qui Jan 03, 2013 20:16
Cálculo: Limites, Derivadas e Integrais
-
- [Funções] Como encontrar f(x) tendo pontos x e y?
por Maschio » Seg Out 08, 2012 13:17
- 6 Respostas
- 5605 Exibições
- Última mensagem por Maschio

Ter Out 09, 2012 12:33
Funções
-
- Como saber se duas funções se interceptam ou não.
por marlonsouza23 » Sex Set 21, 2012 18:48
- 3 Respostas
- 12414 Exibições
- Última mensagem por fraol

Sáb Set 22, 2012 16:04
Funções
-
- AREA LIMITADA
 por ELCIO GOMES DE SOUZA » Dom Ago 24, 2008 16:55
por ELCIO GOMES DE SOUZA » Dom Ago 24, 2008 16:55
- 3 Respostas
- 7165 Exibições
- Última mensagem por admin

Ter Ago 26, 2008 19:02
Cálculo: Limites, Derivadas e Integrais
-
- Integral, área da região limitada.
por Maicon Simoes » Qui Abr 19, 2012 10:58
- 1 Respostas
- 1943 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 15:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e 
 deu
deu ![x=\sqrt[]{3} x=\sqrt[]{3}](/latexrender/pictures/523b5ee3434676b965de6142a602f32d.png) e o segundo ponto
e o segundo ponto
![A=\int_{\sqrt[]{3}}^{3}f(x) - \int_{\sqrt[]{3}}^{3}g(x) A=\int_{\sqrt[]{3}}^{3}f(x) - \int_{\sqrt[]{3}}^{3}g(x)](/latexrender/pictures/abe8d7966e539f2b602391145a49b561.png)

![\int_{\sqrt[]{3}}^{3}|{x}^{2}-4| dx = \int_{\sqrt[]{3}}^{3}|{x}^{2}-4| dx =](/latexrender/pictures/e412dd1ef60eae7419795ac2d206422a.png)
![{x}^{3}/3 - 4x\int_{\sqrt[]{3}}^{3} = {x}^{3}/3 - 4x\int_{\sqrt[]{3}}^{3} =](/latexrender/pictures/df23a7264bb2cbf43a19ee3b358bc621.png)
![{3}^{3}/3 - 4*3-({\sqrt[]{3})^{3}/3 - 4*\sqrt[]{3}) = {3}^{3}/3 - 4*3-({\sqrt[]{3})^{3}/3 - 4*\sqrt[]{3}) =](/latexrender/pictures/3479521adaf56dc257b86d368b481bee.png)


![\int_{\sqrt[]{3}}^{3}2 dx = \int_{\sqrt[]{3}}^{3}2 dx =](/latexrender/pictures/879f8985dad8863b25eb2a3bbf9da463.png)
![2x\int_{\sqrt[]{3}}^{3} = 2x\int_{\sqrt[]{3}}^{3} =](/latexrender/pictures/ebd850547122d61407fd5bc8c78b2b97.png)
![2*3-2 \sqrt[]{3}= 2*3-2 \sqrt[]{3}=](/latexrender/pictures/019e6c441bcd348126ea7938eeb3927b.png)











 e
e  . A 2° função é a Função Constante que não há nenhum detalhe a se preocupar. Já a 1° função temos um módulo envolvido, de forma que teremos de definí-la por partes. Lembre-se que
. A 2° função é a Função Constante que não há nenhum detalhe a se preocupar. Já a 1° função temos um módulo envolvido, de forma que teremos de definí-la por partes. Lembre-se que

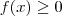 e
e 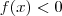 .
.
![\left | x^2-4 \right |=\left\{\begin{matrix}
x^2-4 &,-2 \geq x\geq 2 \\
-x^2 + 4 &, 2> x > -2
\end{matrix}\right. = \left\{\begin{matrix}
x^2-4 &,(-\infty ,-2]\cup [2,\infty ) \\
-x^2 + 4 &, (-2,2)
\end{matrix}\right. \left | x^2-4 \right |=\left\{\begin{matrix}
x^2-4 &,-2 \geq x\geq 2 \\
-x^2 + 4 &, 2> x > -2
\end{matrix}\right. = \left\{\begin{matrix}
x^2-4 &,(-\infty ,-2]\cup [2,\infty ) \\
-x^2 + 4 &, (-2,2)
\end{matrix}\right.](/latexrender/pictures/df9731e660f2591b52871cfe9eed3904.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
