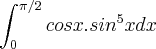 , vou fazer uma prova daqui 2 semanas, com conteúdos mais avançados de calculo 2, mas estou revisando os conceitos gerais, por isso gostaria de ajuda para resolver essa questão, pois errei na prova e não estou conseguindo resolve-la... obrigado!
, vou fazer uma prova daqui 2 semanas, com conteúdos mais avançados de calculo 2, mas estou revisando os conceitos gerais, por isso gostaria de ajuda para resolver essa questão, pois errei na prova e não estou conseguindo resolve-la... obrigado!

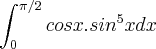 , vou fazer uma prova daqui 2 semanas, com conteúdos mais avançados de calculo 2, mas estou revisando os conceitos gerais, por isso gostaria de ajuda para resolver essa questão, pois errei na prova e não estou conseguindo resolve-la... obrigado!
, vou fazer uma prova daqui 2 semanas, com conteúdos mais avançados de calculo 2, mas estou revisando os conceitos gerais, por isso gostaria de ajuda para resolver essa questão, pois errei na prova e não estou conseguindo resolve-la... obrigado!
gabriel feron escreveu:Fiz uma prova recentemente e caiu a seguinte questão:, vou fazer uma prova daqui 2 semanas, com conteúdos mais avançados de calculo 2, mas estou revisando os conceitos gerais, por isso gostaria de ajuda para resolver essa questão, pois errei na prova e não estou conseguindo resolve-la... obrigado!
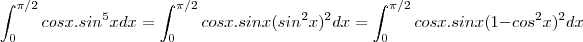
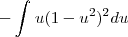

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante