 por menino de ouro » Dom Jan 13, 2013 17:11
por menino de ouro » Dom Jan 13, 2013 17:11
pessoal como faço para calcular e fazer o gráfico dessa questão:
Esboce a região e ache a área da região compreendida entre o gráfico de x =
![\sqrt[]{y} \sqrt[]{y}](/latexrender/pictures/2c7054a0a5416b35c805d1e6e3dc1a54.png)
e as retas
x = y ? 2 e y =0
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por Russman » Dom Jan 13, 2013 19:37
por Russman » Dom Jan 13, 2013 19:37
Primeiramente você deve desenhar as funções e em seguida observar a área que foi "cercada" por elas.
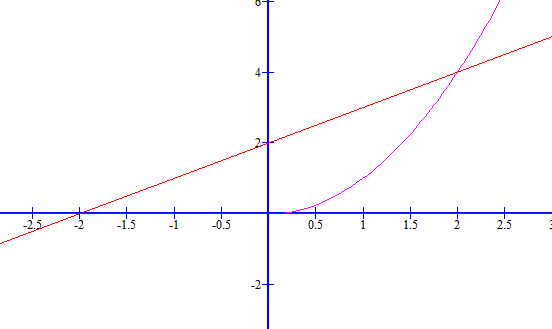
- ScreenHunter_01 Jan. 13 19.13.gif (3.82 KiB) Exibido 9393 vezes
A área varrida vai de

até

, uma vez que a reta
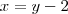
intersecta a

em

e a função

( que só se define para

) intersecta a mesma reta em

.
Demo:
1)
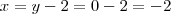
2)

Porem,

gera

que não pertence ao domínio da função. Assim, ficamos com

que pertence.
Podemos agora fazer uma subtração de áreas para calcular a de interesse. Calculamos a área da reta
![[tex]x=y-2 \Rightarrow y=x+2 [tex]x=y-2 \Rightarrow y=x+2](/latexrender/pictures/92344b6743706a082ae47a0ae6e9d5b7.png)
[/tex] de

até

e subtraímos a área de
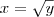
de

até

. Dessa forma,
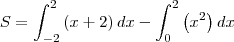
.
Agora basta calcular.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por menino de ouro » Dom Jan 13, 2013 20:47
por menino de ouro » Dom Jan 13, 2013 20:47
qual dessas duas esta correta na expressao( s ) ?

-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por Russman » Dom Jan 13, 2013 20:59
por Russman » Dom Jan 13, 2013 20:59
Estamos integrando em

. Assim, devemos expressar a função integrante como função de

.
Se

então

, para

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por menino de ouro » Dom Jan 13, 2013 21:59
por menino de ouro » Dom Jan 13, 2013 21:59
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por Russman » Dom Jan 13, 2013 22:09
por Russman » Dom Jan 13, 2013 22:09
Calculei o mesmo que você. Mas a resposta em si não importa e sim o raciocínio para tal.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral com aplicaçao
 por menino de ouro » Dom Jan 20, 2013 15:31
por menino de ouro » Dom Jan 20, 2013 15:31
- 6 Respostas
- 4063 Exibições
- Última mensagem por menino de ouro

Qui Jan 24, 2013 23:34
Cálculo: Limites, Derivadas e Integrais
-
- Uma aplicação de Integral(ESFERA)
por CuriosoNerde » Dom Mai 31, 2009 20:00
- 1 Respostas
- 3113 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integral]Aplicação de fórmula
por Matheus Lacombe O » Sáb Mar 30, 2013 18:25
- 5 Respostas
- 4030 Exibições
- Última mensagem por Russman

Dom Mar 31, 2013 21:19
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAL DUPLA - APLICAÇÃO
por sasuyanli » Dom Dez 01, 2013 12:34
- 2 Respostas
- 2299 Exibições
- Última mensagem por sasuyanli

Dom Dez 01, 2013 23:48
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicação de Integral] Área de Revolução
 por carlosce88 » Qua Out 26, 2016 22:40
por carlosce88 » Qua Out 26, 2016 22:40
- 0 Respostas
- 5066 Exibições
- Última mensagem por carlosce88

Qua Out 26, 2016 22:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{y} \sqrt[]{y}](/latexrender/pictures/2c7054a0a5416b35c805d1e6e3dc1a54.png) e as retas
e as retas
![\sqrt[]{y} \sqrt[]{y}](/latexrender/pictures/2c7054a0a5416b35c805d1e6e3dc1a54.png) e as retas
e as retas
 até
até  , uma vez que a reta
, uma vez que a reta 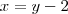 intersecta a
intersecta a  em
em  e a função
e a função  ( que só se define para
( que só se define para  ) intersecta a mesma reta em
) intersecta a mesma reta em  .
. 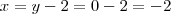

 gera
gera  que não pertence ao domínio da função. Assim, ficamos com
que não pertence ao domínio da função. Assim, ficamos com  que pertence.
que pertence.![[tex]x=y-2 \Rightarrow y=x+2 [tex]x=y-2 \Rightarrow y=x+2](/latexrender/pictures/92344b6743706a082ae47a0ae6e9d5b7.png) [/tex] de
[/tex] de  até
até  e subtraímos a área de
e subtraímos a área de 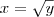 de
de  até
até  . Dessa forma,
. Dessa forma,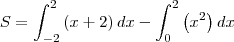 .
.


 . Assim, devemos expressar a função integrante como função de
. Assim, devemos expressar a função integrante como função de  .
.  então
então  , para
, para  .
.
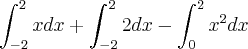
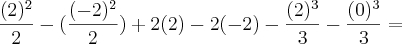
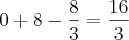




 , avisa que eu resolvo.
, avisa que eu resolvo.

