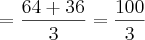por rodrigonapoleao » Qua Dez 26, 2012 13:56
por rodrigonapoleao » Qua Dez 26, 2012 13:56
![\int_{0}^{8}\sqrt[]{2x}+\sqrt[3]{x}dx \int_{0}^{8}\sqrt[]{2x}+\sqrt[3]{x}dx](/latexrender/pictures/8771a0b595f8c1bf2ed34cfb8d5d4d46.png)
. nao sei como resolver por causa da raiz cubica
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por lucas7 » Qua Dez 26, 2012 16:17
por lucas7 » Qua Dez 26, 2012 16:17
calculei e cheguei na resposta 100/3, vou repassar em alguns minutos a minha resolucao para te ajudar. abracos!
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por lucas7 » Qua Dez 26, 2012 16:45
por lucas7 » Qua Dez 26, 2012 16:45
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por DanielFerreira » Sex Dez 28, 2012 21:52
por DanielFerreira » Sex Dez 28, 2012 21:52
Resolução correta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular a Integral de 1/4+x^2
por lucat28 » Sex Ago 12, 2011 15:07
- 5 Respostas
- 7060 Exibições
- Última mensagem por lucat28

Dom Ago 14, 2011 12:43
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] como calcular
por ghiza » Seg Jul 15, 2013 11:23
- 2 Respostas
- 1803 Exibições
- Última mensagem por ghiza

Seg Jul 15, 2013 13:24
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL]Calcular área y=x^2
 por krtc » Qua Jul 24, 2013 02:07
por krtc » Qua Jul 24, 2013 02:07
- 5 Respostas
- 3736 Exibições
- Última mensagem por Russman

Qua Jul 24, 2013 03:13
Cálculo: Limites, Derivadas e Integrais
-
- Calcular a area de uma curva, por integral
por bencz » Qui Ago 25, 2011 00:00
- 5 Respostas
- 3508 Exibições
- Última mensagem por LuizAquino

Sáb Set 03, 2011 21:37
Cálculo: Limites, Derivadas e Integrais
-
- [Integral definida] calcular sua derivada
por Ge_dutra » Dom Mai 12, 2013 21:49
- 0 Respostas
- 1048 Exibições
- Última mensagem por Ge_dutra

Dom Mai 12, 2013 21:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{8}\sqrt[]{2x}+\sqrt[3]{x}dx \int_{0}^{8}\sqrt[]{2x}+\sqrt[3]{x}dx](/latexrender/pictures/8771a0b595f8c1bf2ed34cfb8d5d4d46.png) . nao sei como resolver por causa da raiz cubica
. nao sei como resolver por causa da raiz cubica

![\int_{0}^{8}\sqrt[]{2x}+\sqrt[3]{x}dx \int_{0}^{8}\sqrt[]{2x}+\sqrt[3]{x}dx](/latexrender/pictures/8771a0b595f8c1bf2ed34cfb8d5d4d46.png) . nao sei como resolver por causa da raiz cubica
. nao sei como resolver por causa da raiz cubica

![\int_{0}^{8}\left( \sqrt[2]{2x}+\sqrt[3]{x} \right)dx \int_{0}^{8}\left( \sqrt[2]{2x}+\sqrt[3]{x} \right)dx](/latexrender/pictures/6c09f30735cb45ea3b02442903805546.png)
![= \int_{0}^{8}\left( \sqrt[2]{2}\sqrt[2]{x}+\sqrt[3]{x} \right)dx = \int_{0}^{8}\left( \sqrt[2]{2}\sqrt[2]{x}+\sqrt[3]{x} \right)dx](/latexrender/pictures/bab419f75aacd278db0b907544fa0c57.png)
![=\sqrt[2]{2}\int_{0}^{8}{x}^{1/2}dx + \int_{0}^{8}\sqrt[3]{x}dx =\sqrt[2]{2}\int_{0}^{8}{x}^{1/2}dx + \int_{0}^{8}\sqrt[3]{x}dx](/latexrender/pictures/1b9e7b9c08031da18e6f9ee10da53088.png)
![=\sqrt[2]{2}\int_{0}^{8}{x}^{1/2}dx + \int_{0}^{8}{x}^{1/3}dx =\sqrt[2]{2}\int_{0}^{8}{x}^{1/2}dx + \int_{0}^{8}{x}^{1/3}dx](/latexrender/pictures/23e2abd481f4d1dffa75777778c25c19.png)
![=\sqrt[2]{2}\frac{{x}^{3/2}}{3/2} + \frac{{x}^{4/3}}{4/3} =\sqrt[2]{2}\frac{{x}^{3/2}}{3/2} + \frac{{x}^{4/3}}{4/3}](/latexrender/pictures/b7b9981149f9185cbfb2f53bfe46d266.png) , fazendo x=8 - x=0 temos:
, fazendo x=8 - x=0 temos:![\sqrt[2]{2}\times2\times\frac{\sqrt[2]{{8}^{3}}}{3}+3\times\frac{\sqrt[3]{{8}^{4}}}{4} \sqrt[2]{2}\times2\times\frac{\sqrt[2]{{8}^{3}}}{3}+3\times\frac{\sqrt[3]{{8}^{4}}}{4}](/latexrender/pictures/c03e0bdcda5d3ed4816340ca9f865547.png)
![=\sqrt[2]{2}\times2\times\frac{\sqrt[2]{{8}^{2}\times8}}{3}+3\times\frac{\sqrt[3]{{8}^{3}\times{2}^{3}}}{4} =\sqrt[2]{2}\times2\times\frac{\sqrt[2]{{8}^{2}\times8}}{3}+3\times\frac{\sqrt[3]{{8}^{3}\times{2}^{3}}}{4}](/latexrender/pictures/8ea99f61b289f22dfdfd99bb2214f3a0.png)
![=\sqrt[2]{2}\times2\times8\times\frac{\sqrt[2]{8}}{3}+\frac{3\times8\times2}{4} =\sqrt[2]{2}\times2\times8\times\frac{\sqrt[2]{8}}{3}+\frac{3\times8\times2}{4}](/latexrender/pictures/2cb9fa8d794f431d1c2960ad296ef4f2.png)
![=\frac{16\times\sqrt[2]{16}}{3}+12 =\frac{16\times\sqrt[2]{16}}{3}+12](/latexrender/pictures/905a2c575e41ad92d80e2406ad1ccc19.png)
![=\frac{16\times\sqrt[2]{4\times4}}{3}+12 = \frac{64}{3}+12 =\frac{16\times\sqrt[2]{4\times4}}{3}+12 = \frac{64}{3}+12](/latexrender/pictures/dad8d99dfd17ac9ec6a865fa13e095ff.png)