 por Garota nerd » Dom Nov 25, 2012 23:59
por Garota nerd » Dom Nov 25, 2012 23:59
Equações diferenciais, Alguém poderia me ajudar?
Resolva e equação diferencial(Equações sem a Variável Independente)
y"+y(y')³=0(Sugestão:faça u=y')
resposta: (1/3)y³-2c1y+c2=2t;também y=c
eu fiz o seguinte:
u=y'
u'=du/dx=dudy/dydx=udu/dy
u'=-yu³
udu/dy=-yu³
du/u²=-ydy
-u^-1=-y²dy/2
-1/u=-y²dy/2
1/u=y²dy/2
1/y'=y²dy/2
dx/dy=y²/2
2dx=y²dy
y²dy=2dx
apliquei integral e
y³/3=2xc1+c
y³/3-2c1x-c=0
y³/3-2c1x+c2 onde c2=-c
mas ainda não cheguei na resposta do livro=(
Alguém poderia me ajudar ?
-
Garota nerd
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Mai 03, 2011 17:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Garota nerd » Seg Nov 26, 2012 23:32
por Garota nerd » Seg Nov 26, 2012 23:32
Obrigada, você é uma anjo =)
-
Garota nerd
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Mai 03, 2011 17:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações Diferenciais] De segunda ordem
por palliativos » Dom Nov 16, 2014 20:35
- 1 Respostas
- 1433 Exibições
- Última mensagem por adauto martins

Qua Nov 19, 2014 12:06
Cálculo: Limites, Derivadas e Integrais
-
- Equações matriciais - Resolver em ordem a X
por jmarquesk » Qui Jan 15, 2015 07:39
- 1 Respostas
- 4195 Exibições
- Última mensagem por DanielFerreira

Dom Jun 07, 2015 23:30
Matrizes e Determinantes
-
- Equações diferenciais: ordem, tipo e grau
 por luanavsr » Qui Set 05, 2013 14:56
por luanavsr » Qui Set 05, 2013 14:56
- 0 Respostas
- 1339 Exibições
- Última mensagem por luanavsr

Qui Set 05, 2013 14:56
Cálculo: Limites, Derivadas e Integrais
-
- uma ajudinha aí por favor!!!!!!!!!!!!
por zig » Sex Abr 22, 2011 21:20
- 1 Respostas
- 1700 Exibições
- Última mensagem por Abelardo

Sex Abr 22, 2011 21:37
Sistemas de Equações
-
- Ajudinha prfv
 por juuheuh » Sáb Mai 21, 2016 13:20
por juuheuh » Sáb Mai 21, 2016 13:20
- 1 Respostas
- 1878 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 21, 2016 16:38
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


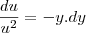
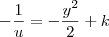

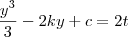

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)