Aqui estou novamente, sofrendo em uma parametrização...
DETERMINE UMA FUNÇÃO DE UM PARÂMETRO t CUJA IMAGEM É UMA ELIPSE COM CENTRO EM (0,0) E TAL QUE, EM t = 0, O VETOR TANGENTE É HORIZONTAL DE NORMA 2 E NO INSTANTE pi/2 O VETOR TANGENTE A CURVA É VERTICAL DE NORMA 3.
Sei que a parametrização de uma elipse de centro 0,0 pode ser algo como:
w(t) = (a cost, b sent)
e sua derivada (vetor tangente a curva)
w'(t) = (-a sent, b cost)
mas não entendi o que devo fazer, a partir daí, com os dados fornecidos.
Agradeço toda e qualquer ajuda!!
abraços (:



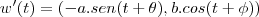

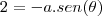
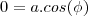
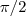 temos w'(t)=(0,3)
temos w'(t)=(0,3)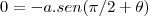
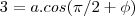

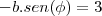
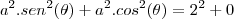
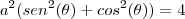
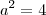

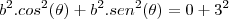
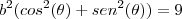




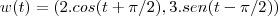


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)