C(t) =
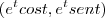
DEMONSTRE QUE O VETOR TANGENTE À TRAJETÓRIA FAZ UM ÂNGULO CONSTANTE DE pi/4 COM O VETOR POSIÇÃO.
Minha tentativa:
Sei que o vetor tangente a trajetória é a derivada de C(t), então foi o que fiz, chegando em:
C'(t) =
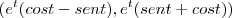
Tenho então o vetor tangente a trajetória. Agora como provo que o angulo entre ele e o vetor posição é pi/4??
Desde já, agradeço!!



 ,
,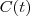 é
é 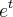 . Calcule
. Calcule 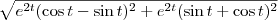
 ,
, 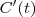 e o produto escalar
e o produto escalar 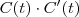 respectivamente, e substitua na equação.
respectivamente, e substitua na equação.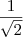 .
.


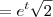 ,
,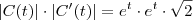 .
.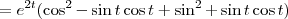
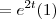 .
.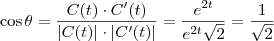 .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)