 por robsonpds » Seg Nov 19, 2012 19:54
por robsonpds » Seg Nov 19, 2012 19:54
-
robsonpds
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Nov 19, 2012 05:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Seg Nov 19, 2012 20:24
por e8group » Seg Nov 19, 2012 20:24
Boa noite . Antes de tudo , divida cada termos por

. Lembre que ,

é o mesmo que ,

, ou seja ,

Se não conseguir post algo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por robsonpds » Seg Nov 19, 2012 22:25
por robsonpds » Seg Nov 19, 2012 22:25
santhiago escreveu:Boa noite . Antes de tudo , divida cada termos por

. Lembre que ,

é o mesmo que ,

, ou seja ,

Se não conseguir post algo .
Santhiago eu até cheguei ai, só o meu resultado final meu não bate que é 0.9566, você poderia me ajudar eu estou deixando assim

-
robsonpds
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Nov 19, 2012 05:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Ter Nov 20, 2012 07:22
por e8group » Ter Nov 20, 2012 07:22
Bom dia .

Daí,
![F(x )= \int (1 - x^{-3} + x^{-4})dx = \int dx - \int x^{-3} dx + \int x^{-4}dx = x + x^{-2}/2 - x^{-3}/3 + c = x + \frac{1}{2x^2} - \frac{1}{3x^3} + c = \frac{6x^4 - 3x - 2}{6x^3} + c \\ \\
\int_2^3 f'(x) dx = F(3) - F(2) = \frac{6(3^4)- 3(3)-2}{6(3^3)} -\frac{[6(2^4)- 3(2)-2]}{6(2^3)} = \frac{475}{162} - \frac{11}{6} = \frac{475 - 11 \cdot 27}{162} = \frac{475 - 297}{162} = \frac{178}{162} = \frac{89}{81} \approx 1,1 F(x )= \int (1 - x^{-3} + x^{-4})dx = \int dx - \int x^{-3} dx + \int x^{-4}dx = x + x^{-2}/2 - x^{-3}/3 + c = x + \frac{1}{2x^2} - \frac{1}{3x^3} + c = \frac{6x^4 - 3x - 2}{6x^3} + c \\ \\
\int_2^3 f'(x) dx = F(3) - F(2) = \frac{6(3^4)- 3(3)-2}{6(3^3)} -\frac{[6(2^4)- 3(2)-2]}{6(2^3)} = \frac{475}{162} - \frac{11}{6} = \frac{475 - 11 \cdot 27}{162} = \frac{475 - 297}{162} = \frac{178}{162} = \frac{89}{81} \approx 1,1](/latexrender/pictures/3cace8be6f1aaea09540413b19e22a35.png)
Realmente o resultado difere da aproximação que é 0.9566 . Para termos um número postivo e menor que um . O numerador teria de ser menor que o denominador .
talvez eu errei algum calculo , fiz sem calculadora .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Ter Nov 20, 2012 09:58
por MarceloFantini » Ter Nov 20, 2012 09:58
Robson, vamos esclarecer algo:
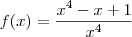
e você quer calcular
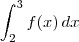
?
A resposta do
Wolfram bate. Clique para ver a solução passo a passo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Ter Nov 20, 2012 17:02
por e8group » Ter Nov 20, 2012 17:02
Desculpe , erei o sinal ao digitar a resposta da integral , é só trocar o sinal de menos para mais que estará tudo certo .
o certo é :
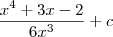
e não

como estava anteriormente . Agora é só calcular ,

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por robsonpds » Ter Nov 20, 2012 19:36
por robsonpds » Ter Nov 20, 2012 19:36
santhiago escreveu:Desculpe , erei o sinal ao digitar a resposta da integral , é só trocar o sinal de menos para mais que estará tudo certo .
o certo é :
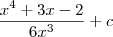
e não

como estava anteriormente . Agora é só calcular ,

.
santhiago escreveu:Desculpe , erei o sinal ao digitar a resposta da integral , é só trocar o sinal de menos para mais que estará tudo certo .
o certo é :
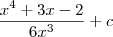
e não

como estava anteriormente . Agora é só calcular ,

.
ok santhiago, agora o resultado bate, valeu muito obrigado pela força.
-
robsonpds
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Nov 19, 2012 05:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4214 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3535 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 2943 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2412 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3487 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 . Lembre que ,
. Lembre que ,  é o mesmo que ,
é o mesmo que ,  , ou seja ,
, ou seja , 

. Lembre que ,
é o mesmo que ,
, ou seja ,




![F(x )= \int (1 - x^{-3} + x^{-4})dx = \int dx - \int x^{-3} dx + \int x^{-4}dx = x + x^{-2}/2 - x^{-3}/3 + c = x + \frac{1}{2x^2} - \frac{1}{3x^3} + c = \frac{6x^4 - 3x - 2}{6x^3} + c \\ \\
\int_2^3 f'(x) dx = F(3) - F(2) = \frac{6(3^4)- 3(3)-2}{6(3^3)} -\frac{[6(2^4)- 3(2)-2]}{6(2^3)} = \frac{475}{162} - \frac{11}{6} = \frac{475 - 11 \cdot 27}{162} = \frac{475 - 297}{162} = \frac{178}{162} = \frac{89}{81} \approx 1,1 F(x )= \int (1 - x^{-3} + x^{-4})dx = \int dx - \int x^{-3} dx + \int x^{-4}dx = x + x^{-2}/2 - x^{-3}/3 + c = x + \frac{1}{2x^2} - \frac{1}{3x^3} + c = \frac{6x^4 - 3x - 2}{6x^3} + c \\ \\
\int_2^3 f'(x) dx = F(3) - F(2) = \frac{6(3^4)- 3(3)-2}{6(3^3)} -\frac{[6(2^4)- 3(2)-2]}{6(2^3)} = \frac{475}{162} - \frac{11}{6} = \frac{475 - 11 \cdot 27}{162} = \frac{475 - 297}{162} = \frac{178}{162} = \frac{89}{81} \approx 1,1](/latexrender/pictures/3cace8be6f1aaea09540413b19e22a35.png)

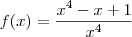
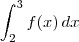 ?
?

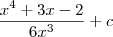 e não
e não  como estava anteriormente . Agora é só calcular ,
como estava anteriormente . Agora é só calcular ,  .
.
e não
como estava anteriormente . Agora é só calcular ,
.
e não
como estava anteriormente . Agora é só calcular ,
.
