 por Bianca_R » Dom Nov 04, 2012 17:17
por Bianca_R » Dom Nov 04, 2012 17:17
Olá,
estou com muita dúvida na seguinte questão:
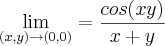
A resposta é que o limite não existe mas não consigo chegar nessa solução. Já tentei fazer

e
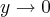
, por dois caminhos:
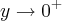
e
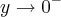
Tentei também utilizar como caminhos algumas equações como
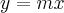
,

e etc.
Alguém pode por favor me ajudar e dizer o que estou fazendo de errado e qual caminho devo seguir ?
-
Bianca_R
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Nov 04, 2012 17:03
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Dom Nov 04, 2012 19:37
por MarceloFantini » Dom Nov 04, 2012 19:37
Este seu primeiro caminho não está errado. Tomando

temos que
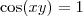
e
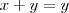
. Portanto sobra o limite
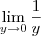
. Se
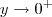
então o limite será

, enquanto que se

então o limite será
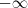
.
Disso concluímos que o limite não existe.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite]Limite de uma funçao de varias variaveis
por TheKyabu » Seg Fev 04, 2013 22:01
- 3 Respostas
- 3465 Exibições
- Última mensagem por young_jedi

Ter Fev 05, 2013 19:47
Cálculo: Limites, Derivadas e Integrais
-
- Limite de várias variáveis
por braddock » Seg Mai 05, 2014 04:06
- 2 Respostas
- 5031 Exibições
- Última mensagem por braddock

Seg Mai 05, 2014 22:17
Cálculo
-
- [Limites] Equação de limite de duas variáveis reais
por Bianca_R » Dom Nov 04, 2012 21:45
- 1 Respostas
- 2157 Exibições
- Última mensagem por e8group

Seg Nov 05, 2012 11:19
Cálculo: Limites, Derivadas e Integrais
-
- Limites de funções com varias variáveis
por Fernandobertolaccini » Qua Dez 17, 2014 10:49
- 1 Respostas
- 3752 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 13:59
Cálculo: Limites, Derivadas e Integrais
-
- Limites de funções com varias variáveis
por Fernandobertolaccini » Qua Dez 17, 2014 10:56
- 1 Respostas
- 3186 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 14:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
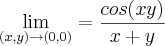
 e
e 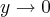 , por dois caminhos:
, por dois caminhos: 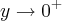 e
e 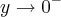
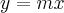 ,
,  e etc.
e etc.

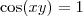 e
e 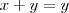 . Portanto sobra o limite
. Portanto sobra o limite 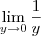 . Se
. Se 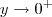 então o limite será
então o limite será  , enquanto que se
, enquanto que se  então o limite será
então o limite será 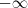 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.