![\lim_{x\rightarrow0}\left[\frac{tan(7x)}{sen(3x)} \right]=? \lim_{x\rightarrow0}\left[\frac{tan(7x)}{sen(3x)} \right]=?](/latexrender/pictures/23f54054764f3dab4148ca9dc00ea707.png)
-Tentei utilizar a propriedade a seguir, mas não consegui chegar a uma reposta:
Propriedade:
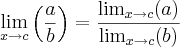
![\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{sen(3x)} \right] = \frac{\lim_{x\rightarrow 0}\left[tan(7x)\right] }{\lim_{x\rightarrow 0} \left[sen(3x)\right]} \lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{sen(3x)} \right] = \frac{\lim_{x\rightarrow 0}\left[tan(7x)\right] }{\lim_{x\rightarrow 0} \left[sen(3x)\right]}](/latexrender/pictures/08d6523d3981b59e65805bc4896e80a0.png)
- Tentei também:
![\lim_{x\rightarrow 0}\left[ \frac{ \frac{sen(7x)}{cos(7x)}}{ \frac{sen(3x)}{1}}\right] = \lim_{x\rightarrow 0}\left[ \frac{sen(7x)}{cos(7x)}. \frac{1}{sen(3x)}\right] \lim_{x\rightarrow 0}\left[ \frac{ \frac{sen(7x)}{cos(7x)}}{ \frac{sen(3x)}{1}}\right] = \lim_{x\rightarrow 0}\left[ \frac{sen(7x)}{cos(7x)}. \frac{1}{sen(3x)}\right]](/latexrender/pictures/47473adc12536a3a69546624ee1375ba.png)
- E, considerando a propriedade abaixo:
Propriedade:
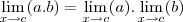
![= \lim_{x\rightarrow 0}\left[ \frac{sen(7x)}{cos(7x)} \right].\lim_{x\rightarrow 0}\left[ \frac{1}{sen(3x)} \right] = \lim_{x\rightarrow 0}\left[ \frac{sen(7x)}{cos(7x)} \right].\lim_{x\rightarrow 0}\left[ \frac{1}{sen(3x)} \right]](/latexrender/pictures/f151ab729959cbdfd165e97615ec0881.png)
- Olha, o senhores me desculpem se a dúvida é idota, mas realmente travei, astá tudo muito confuso nesse conteúdo de limites, perece que o critério que aplicado a uma resolução não se aplica à outra e assim por diante. E ainda para piorar peguei um professor "matão" que já nos deu não sei quantos desfalques, passou a lista "em cima do laço" e não marcou reposição das aulas, sendo ainda que a prova continua na mesma data. Vixe, aqui ta foda. A primeira prova fui poliposition, mas do jeito que esse conteúdo aqui ficou nas coxas. Bem, enfim, se alguém puder dar uma exclarecida ou recomendar um bom site sobre o conteúdo, fico grato. Preciso en-ten-der este exercicío.
- Por favor, o que está faltando eu conhecer para resolver este exercicío?
OBS: A resposta do gabarito é (7/3) = 2.33333... Conferi pelo Microsoft Mathematics e a resposta de fato bate. Só não consigo chegar a ela.


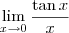 . Este limite é 1. Para provar isto, perceba que
. Este limite é 1. Para provar isto, perceba que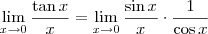
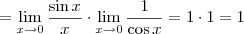 .
.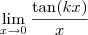 , com
, com 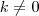 , este limite será
, este limite será  por considerações semelhantes.
por considerações semelhantes.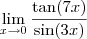 . Multiplique e divida por
. Multiplique e divida por  , então
, então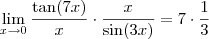 .
.

![\lim_{x\rightarrow 0}\left[ \frac{tan(ax)}{x} \right]=a.1 \lim_{x\rightarrow 0}\left[ \frac{tan(ax)}{x} \right]=a.1](/latexrender/pictures/98e665bbc30edfe0920fb0d479697af6.png)
![\lim_{x\rightarrow 0}\left[ \frac{sen(ax)}{x} \right]=a.1 \lim_{x\rightarrow 0}\left[ \frac{sen(ax)}{x} \right]=a.1](/latexrender/pictures/d7a35fdba454b5fbcbf28a75bb306f2b.png)
![\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{sen(3x)} \right]= \lim_{x\rightarrow 0}\left[ \frac{ \frac{tan(7x)}{x} }{ \frac{sen(3x)}{x} } \right]=\lim_{x\rightarrow 0}\left[ \frac{ 7 }{ 3 } \right]=\left[ \frac{\lim_{x\rightarrow 0}(7) }{\lim_{x\rightarrow 0}(3)} \right]=\frac{7}{3} \lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{sen(3x)} \right]= \lim_{x\rightarrow 0}\left[ \frac{ \frac{tan(7x)}{x} }{ \frac{sen(3x)}{x} } \right]=\lim_{x\rightarrow 0}\left[ \frac{ 7 }{ 3 } \right]=\left[ \frac{\lim_{x\rightarrow 0}(7) }{\lim_{x\rightarrow 0}(3)} \right]=\frac{7}{3}](/latexrender/pictures/067525699c17067508095aa2aea84317.png)
![\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{sen(3x)} \right]= \lim_{x\rightarrow 0}\left[ \frac{ \frac{tan(7x)}{1} }{ \frac{sen(3x)}{1} } \right]=\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{1}.\frac{1}{sen(3x)} \right]= \lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{sen(3x)} \right]= \lim_{x\rightarrow 0}\left[ \frac{ \frac{tan(7x)}{1} }{ \frac{sen(3x)}{1} } \right]=\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{1}.\frac{1}{sen(3x)} \right]=](/latexrender/pictures/0fb26bc8df6271dcf0427a9e098dabb6.png)
![\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{1.x}.\frac{1.x}{sen(3x)} \right]=\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{x}.\frac{x}{sen(3x)} \right]=\lim_{x\rightarrow 0}\left[\frac{7}{1}.\frac{1}{3} \right]=\lim_{x\rightarrow 0}\left[\frac{7}{3} \right] \lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{1.x}.\frac{1.x}{sen(3x)} \right]=\lim_{x\rightarrow 0}\left[ \frac{tan(7x)}{x}.\frac{x}{sen(3x)} \right]=\lim_{x\rightarrow 0}\left[\frac{7}{1}.\frac{1}{3} \right]=\lim_{x\rightarrow 0}\left[\frac{7}{3} \right]](/latexrender/pictures/1332f68425ae36b9f31f425eaea8e7be.png)
![=\left[ \frac{\lim_{x\rightarrow 0}(7) }{\lim_{x\rightarrow 0}(3)} \right]=\frac{7}{3} =\left[ \frac{\lim_{x\rightarrow 0}(7) }{\lim_{x\rightarrow 0}(3)} \right]=\frac{7}{3}](/latexrender/pictures/05aeea67e3acd3aa75bc6722e74ee52e.png)
![\lim_{x\rightarrow 0}\left[\frac{x}{sen(ax)} \right]= \frac{1}{a.x} \lim_{x\rightarrow 0}\left[\frac{x}{sen(ax)} \right]= \frac{1}{a.x}](/latexrender/pictures/166b986375fa2e53c5287c2764edaaf6.png)
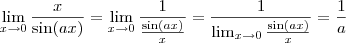 ,
,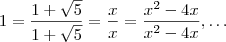 ,
,
 .
.



