 por cristian9192 » Sáb Out 20, 2012 19:06
por cristian9192 » Sáb Out 20, 2012 19:06
Não consigo resolver essa integral.
![\int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-y^2}}(x^2+y^2)^{3/2}dxdy \int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-y^2}}(x^2+y^2)^{3/2}dxdy](/latexrender/pictures/c8e2fc0c32229851729d0d0cff47eb9f.png)
Já tentei usar cordenadas polares, mais não consegui resolver, se alguém poder me ajudar acradeço.
-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sáb Out 20, 2012 21:40
por young_jedi » Sáb Out 20, 2012 21:40
analisando a integral percebemos que ela é limitada pelo um quarto de circunferencia situada no primeiro quadrande do plano xy e que tem raio a.
então passando para coordenadas polares
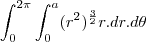
melhorando
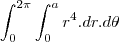
essa integral é mais simples de resolver
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral Tripla (trasformação trigonométrica)
por cristian9192 » Qui Out 25, 2012 14:02
- 4 Respostas
- 2196 Exibições
- Última mensagem por cristian9192

Qui Out 25, 2012 15:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2735 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 2
por DanielFerreira » Dom Mar 18, 2012 12:44
- 5 Respostas
- 3959 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 22:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 4
 por DanielFerreira » Sex Abr 06, 2012 19:49
por DanielFerreira » Sex Abr 06, 2012 19:49
- 4 Respostas
- 2954 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 21:05
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 5
por DanielFerreira » Sex Abr 06, 2012 20:00
- 2 Respostas
- 1803 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-y^2}}(x^2+y^2)^{3/2}dxdy \int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-y^2}}(x^2+y^2)^{3/2}dxdy](/latexrender/pictures/c8e2fc0c32229851729d0d0cff47eb9f.png)

![\int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-y^2}}(x^2+y^2)^{3/2}dxdy \int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-y^2}}(x^2+y^2)^{3/2}dxdy](/latexrender/pictures/c8e2fc0c32229851729d0d0cff47eb9f.png)

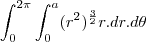
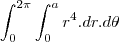

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.