 por iceman » Dom Set 16, 2012 20:05
por iceman » Dom Set 16, 2012 20:05
A função horária de um móvel é definida por
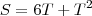
, qual o espaço percorrido quando:
a)T= 0 Seg
b)T= 1 Seg
c)T= 2 Seg
Alguém ajuda, por favor ?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Dom Set 16, 2012 20:34
por Renato_RJ » Dom Set 16, 2012 20:34
Boa noite !!!!
Seguinte, essa função é a função horária da posição ?? Pois se for, não precisa derivar, basta aplicar os valores.....
Agora, se você quer a velocidade da partícula nos instantes dados (a função horária da velocidade), então vai precisar derivar a função. Veja:
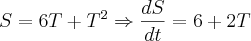
Agora é aplicar os valores...
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por iceman » Dom Set 16, 2012 20:42
por iceman » Dom Set 16, 2012 20:42
Renato_RJ escreveu:Boa noite !!!!
Seguinte, essa função é a função horária da posição ?? Pois se for, não precisa derivar, basta aplicar os valores.....
Agora, se você quer a velocidade da partícula nos instantes dados (a função horária da velocidade), então vai precisar derivar a função. Veja:
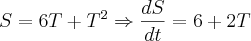
Agora é aplicar os valores...
Abraços,
Renato.
A questão só fala isso....
Eu fiz assim, poderia ver se está certo?
6.0 + 2.0 = 0
6.1 + 2.1 = 9
6.2+2.2 = 16
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Dom Set 16, 2012 20:49
por Renato_RJ » Dom Set 16, 2012 20:49
iceman escreveu:Renato_RJ escreveu:Boa noite !!!!
Seguinte, essa função é a função horária da posição ?? Pois se for, não precisa derivar, basta aplicar os valores.....
Agora, se você quer a velocidade da partícula nos instantes dados (a função horária da velocidade), então vai precisar derivar a função. Veja:
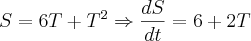
Agora é aplicar os valores...
Abraços,
Renato.
A questão só fala isso....
Eu fiz assim, poderia ver se está certo?
6.0 + 2.0 = 0
6.1 + 2.1 = 9
6.2+2.2 = 16
Campeão, se o problema dá a função horária da posição e pede a velocidade nos instantes dados, então você cometeu um engano pequeno, lembre-se que calculamos
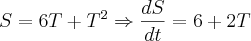
, então não precisa multiplicar o 6 pela variável T (olha a derivada como ficou)....
[ ]'s
Renato..
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema com Derivada
por veldri » Qua Jun 02, 2010 13:51
- 0 Respostas
- 1065 Exibições
- Última mensagem por veldri

Qua Jun 02, 2010 13:51
Cálculo: Limites, Derivadas e Integrais
-
- Problema derivada
 por Herrero088 » Seg Jul 12, 2010 23:31
por Herrero088 » Seg Jul 12, 2010 23:31
- 2 Respostas
- 2707 Exibições
- Última mensagem por Douglasm

Ter Jul 13, 2010 19:47
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Problema [2]
por iceman » Dom Set 16, 2012 21:07
- 6 Respostas
- 2674 Exibições
- Última mensagem por iceman

Dom Set 16, 2012 22:15
Cálculo: Limites, Derivadas e Integrais
-
- Problema com resolução da derivada de uma função
por DavidUserCalc » Qua Mar 31, 2010 19:50
- 2 Respostas
- 3196 Exibições
- Última mensagem por DavidUserCalc

Qui Abr 01, 2010 01:19
Cálculo: Limites, Derivadas e Integrais
-
- Problema com a derivada de uma função composta
por DavidUserCalc » Qui Abr 01, 2010 14:44
- 1 Respostas
- 1956 Exibições
- Última mensagem por Molina

Qui Abr 01, 2010 16:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
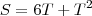 , qual o espaço percorrido quando:
, qual o espaço percorrido quando:
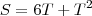 , qual o espaço percorrido quando:
, qual o espaço percorrido quando:
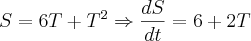


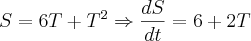 , então não precisa multiplicar o 6 pela variável T (olha a derivada como ficou)....
, então não precisa multiplicar o 6 pela variável T (olha a derivada como ficou)....