 por citadp » Qua Jun 20, 2012 09:32
por citadp » Qua Jun 20, 2012 09:32
Tenho também uma dúvida acerca de raízes.
Tenho uma função x^6+3x^5 = -1
Pedem-me, mostre que a equação tem uma raiz em ]-1, 0 [
Ora, o que eu costumo fazer é derivar, o que me dá 6x^5+ 15x^4
Como não consigo calcular assim os zeros, simplifiquei : x^3(x^2 + 15x) = 0 o que me dá um zero em x=-15, o que supostamente me ensinaram foi que se a derivada não tiver zeros existe apenas um zero na função.
Assim a derivada tem zeros.
Alguém me pode ajudar a resolver isto ?
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
 por Russman » Qua Jun 20, 2012 10:47
por Russman » Qua Jun 20, 2012 10:47
citadp escreveu:Tenho uma função equação x^6+3x^5 = -1
Pedem-me, mostre que a equação tem uma raiz em ]-1, 0 [
Veja que para existir tal raíz a função
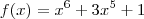
deve mudar de sinal entre
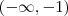
e

Então, para isto, basta selecionar um valor de
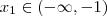
e outro de
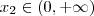
e mostrar que
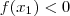
e
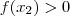
.
Para
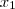
eu escolho, por exemplo

. Assim,
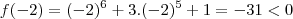
.
Para
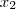
eu escolho, por exemplo

. Assim,
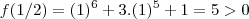
.
Logo, concluímos que existe uma raíz no intervalo

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por citadp » Qua Jun 20, 2012 10:54
por citadp » Qua Jun 20, 2012 10:54
Então não é necessário fazer a derivada da função neste caso ?
E quando nos pedem para mostrar que a função tem no máximo duas raízes ou exactamente duas raízes reais?
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
 por Russman » Sex Jul 06, 2012 15:49
por Russman » Sex Jul 06, 2012 15:49
citadp escreveu:Então não é necessário fazer a derivada da função neste caso ?
Não! Se a função é contínua então na troca de sinais ela precisa necessariamente passar pelo zero.
citadp escreveu:E quando nos pedem para mostrar que a função tem no máximo duas raízes ou exactamente duas raízes reais?
Depende da função que você estudará!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8120 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- Raizes de equação de grau>=3
por spyderkill » Qua Mai 09, 2012 17:31
- 2 Respostas
- 2427 Exibições
- Última mensagem por pedroaugustox47

Sex Mai 11, 2012 02:33
Polinômios
-
- Raizes da equaçao do 2° grau
por hissamo » Sex Abr 10, 2015 15:57
- 1 Respostas
- 1835 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 11, 2015 17:14
Equações
-
- Raizes de uma equação de terceiro grau.
por 380625 » Dom Mar 27, 2011 13:58
- 3 Respostas
- 3017 Exibições
- Última mensagem por MarceloFantini

Dom Mar 27, 2011 18:09
Funções
-
- equação de segundo grau( descobrindo as raizes)
por arturmedeiros2010 » Qui Fev 13, 2014 15:34
- 1 Respostas
- 1362 Exibições
- Última mensagem por Russman

Sex Fev 14, 2014 00:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


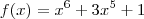 deve mudar de sinal entre
deve mudar de sinal entre 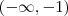 e
e 
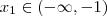 e outro de
e outro de 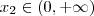 e mostrar que
e mostrar que 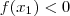 e
e 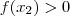 .
.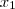 eu escolho, por exemplo
eu escolho, por exemplo  . Assim,
. Assim,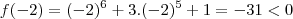 .
.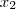 eu escolho, por exemplo
eu escolho, por exemplo  . Assim,
. Assim,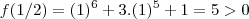 .
. .
.