 por Cleyson007 » Qua Mai 16, 2012 11:41
por Cleyson007 » Qua Mai 16, 2012 11:41
Bom dia a todos!
Calcule
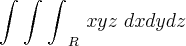
, onde R = [0,1] x [1,2] x [0,3].
A montagem é essa mesma? -->
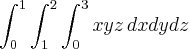
Como resolver esse exercício?
Se alguém puder me ajudar, agradeço.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Qua Mai 16, 2012 15:31
por Cleyson007 » Qua Mai 16, 2012 15:31
Boa tarde a todos!
Parti da montagem acima e consegui desenvolver encontrando 27/8 como resposta

Agora minha dúvida é: Como fazer o esboço da região R de integração?
Aguardando..
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Sex Mai 18, 2012 20:14
por LuizAquino » Sex Mai 18, 2012 20:14
Cleyson007 escreveu:Calcule
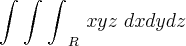
, onde R = [0,1] x [1,2] x [0,3].
A montagem é essa mesma? -->
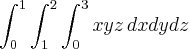
Note a sequência de diferenciais que aparecem na integral: dxdydz.
Desse modo, primeiro estamos integrando em relação a x, depois em relação a y e por fim em relação a z. Como
![R = [0,\, 1]\times [1,\,2]\times [0,\,3] R = [0,\, 1]\times [1,\,2]\times [0,\,3]](/latexrender/pictures/c6e69c0f03a3ae0b7c35b0974c86802d.png)
, temos que
![x\in [0,\,1] x\in [0,\,1]](/latexrender/pictures/ef8197ad111bb26b1ba2c2e33d2480ed.png)
,
![y\in [1,\,2] y\in [1,\,2]](/latexrender/pictures/0fe5417a13b60d1455a53b892c99c5b5.png)
e
![z\in [0,\,3] z\in [0,\,3]](/latexrender/pictures/5b7b47d478ceea320650fc06536e0052.png)
.
Portanto, a montagem adequada é:

Cleyson007 escreveu:Agora minha dúvida é: Como fazer o esboço da região R de integração?
É apenas um prima regular com base quadrada.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral tripla
por DanielFerreira » Dom Jun 10, 2012 19:27
- 1 Respostas
- 1700 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 00:39
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAL TRIPLA
por Garota nerd » Qua Jun 27, 2012 17:40
- 4 Respostas
- 3134 Exibições
- Última mensagem por Garota nerd

Qui Jun 28, 2012 01:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral tripla
por DanielFerreira » Sáb Jul 07, 2012 13:00
- 2 Respostas
- 1877 Exibições
- Última mensagem por DanielFerreira

Dom Jul 08, 2012 13:01
Cálculo: Limites, Derivadas e Integrais
-
- Integral Tripla
por Aniinha » Qua Fev 13, 2013 17:45
- 3 Respostas
- 2212 Exibições
- Última mensagem por young_jedi

Sex Fev 15, 2013 10:33
Cálculo: Limites, Derivadas e Integrais
-
- Integral Tripla!
por samysoares » Sáb Nov 09, 2013 00:23
- 1 Respostas
- 1316 Exibições
- Última mensagem por Man Utd

Sex Nov 15, 2013 15:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
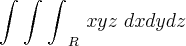 , onde R = [0,1] x [1,2] x [0,3].
, onde R = [0,1] x [1,2] x [0,3].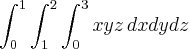

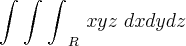 , onde R = [0,1] x [1,2] x [0,3].
, onde R = [0,1] x [1,2] x [0,3].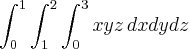



, onde R = [0,1] x [1,2] x [0,3].
![R = [0,\, 1]\times [1,\,2]\times [0,\,3] R = [0,\, 1]\times [1,\,2]\times [0,\,3]](/latexrender/pictures/c6e69c0f03a3ae0b7c35b0974c86802d.png) , temos que
, temos que ![x\in [0,\,1] x\in [0,\,1]](/latexrender/pictures/ef8197ad111bb26b1ba2c2e33d2480ed.png) ,
, ![y\in [1,\,2] y\in [1,\,2]](/latexrender/pictures/0fe5417a13b60d1455a53b892c99c5b5.png) e
e ![z\in [0,\,3] z\in [0,\,3]](/latexrender/pictures/5b7b47d478ceea320650fc06536e0052.png) .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.