 por yonara » Ter Jun 30, 2009 20:19
por yonara » Ter Jun 30, 2009 20:19
Pessoal, esta questão está no meu trabalho, quero pedir a ajuda de vcs, pq me desculpem, mas eu não sei nem começar a fazer...

Determine todos os pontos onde a função
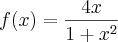
possui extremo relativo e esboce o seu gráfico.
-
yonara
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Jun 30, 2009 18:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: medicina veterinária
- Andamento: cursando
 por Felipe Schucman » Seg Ago 03, 2009 21:15
por Felipe Schucman » Seg Ago 03, 2009 21:15
Para derivar essa função precisamos usar a formula de derivação de um quociente (f(x)/g(x) )?= (f?(x)g(x) ? f(x)g?(x))/g(x)^2
yonara escreveu:Pessoal, esta questão está no meu trabalho, quero pedir a ajuda de vcs, pq me desculpem, mas eu não sei nem começar a fazer...

Determine todos os pontos onde a função
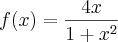
possui extremo relativo e esboce o seu gráfico.
Assim aplicando a formula fica assim
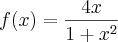
----> f´(x)= (4*(1+x^2) ? 4x*2x)/ (1+x^2)^2. Simplificando essa expressão e igualando a zero você tera os pontos criticos falta testar se são maximo e minimos(pois podem ser pontos de inflexão apenas) e se estão dentro do dominio, e pronto você tera a resposta!
Um abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Desafio: função real]Determinar a função f(x)
por raimundosar » Qui Mai 05, 2016 19:02
- 1 Respostas
- 2466 Exibições
- Última mensagem por nakagumahissao

Sex Mai 06, 2016 00:25
Funções
-
- Determinar Função
por Tonga » Qui Jan 05, 2012 11:43
- 2 Respostas
- 1630 Exibições
- Última mensagem por Tonga

Qui Jan 05, 2012 18:28
Funções
-
- determinar se é função
por virginia » Qui Abr 25, 2013 13:43
- 3 Respostas
- 1642 Exibições
- Última mensagem por e8group

Sex Abr 26, 2013 16:04
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2412 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- função. determinar o seno de y
por franciscokael » Qui Out 21, 2010 15:48
- 1 Respostas
- 1355 Exibições
- Última mensagem por MarceloFantini

Qui Out 21, 2010 18:15
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
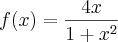 possui extremo relativo e esboce o seu gráfico.
possui extremo relativo e esboce o seu gráfico.
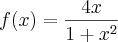 possui extremo relativo e esboce o seu gráfico.
possui extremo relativo e esboce o seu gráfico.

possui extremo relativo e esboce o seu gráfico.
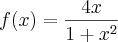 ----> f´(x)= (4*(1+x^2) ? 4x*2x)/ (1+x^2)^2. Simplificando essa expressão e igualando a zero você tera os pontos criticos falta testar se são maximo e minimos(pois podem ser pontos de inflexão apenas) e se estão dentro do dominio, e pronto você tera a resposta!
----> f´(x)= (4*(1+x^2) ? 4x*2x)/ (1+x^2)^2. Simplificando essa expressão e igualando a zero você tera os pontos criticos falta testar se são maximo e minimos(pois podem ser pontos de inflexão apenas) e se estão dentro do dominio, e pronto você tera a resposta!
