Estou com um pequeno problema em Cálculo numérico. Estou com um programa que rodo no force para a função do SENO. Só que estou com dificuldades para passá-la para COSSENO. Sou iniciante em cálculo numérico, se alguém puder me explicar como eu mudo para o COSSENO eu agradeceria. Eu ja entendi todo o funcionamento do código, porém estou errando em trocar a função.
Segue abaixo o código.
c #############################################################
c Este programa calcula o erro percentual da Serie de Taylor da
c funcaoo sen(bx), expandida no ponto x0
implicit double precision(a-h,o-z)
dimension a(50)
open(5,file='taylor01.1',status='old')
open(6,file='taylor200510.2',status='unknown')
c Ponto de expansao da s‚rie
read(5,*)x0
c Grau da s‚rie polinomial + 1
read(5,*)n_termos
c Coeficiente multiplicador do angulo x
read(5,*)b
c Numero de abscissas
read(5,*)n_x
c Impressao do cabecalho
write(6,5)
c determinacao dos coeficientes da serie de Taylor
do n=1,n_termos
i=1
if(mod(n-1,2).eq.0) then !par
j=1
k=0
if(mod(n-1,4).eq.0) then !múltiplo de 4
i=2
endif
else !ímpar
j=0
k=1
if(mod((n-2),4).eq.0) then !múltiplo de 4 + 1
i=2
endif
endif
a(n)=(-1.d0)**i*b**(n-1)*sin(b*x0)**j*cos(b*x0)**k
enddo
do icont=1,n_x
c Leitura das abscissas em arquivo
read(5,*) x
fxt=0.d0
do n=1,n_termos
c solucao num‚rica
fxt=fxt+a(n)*(x-x0)**(n-1)/fat(n-1)
enddo
c solução analítica
fxa=sin(b*x)
c erro percentual
if(fxa.ne.0.d0) then
erro_p=abs((fxt-fxa)/fxa)*100.d0
write(6,15)x,fxa,fxt,erro_p
else
write(6,20)x,fxa,fxt
endif
enddo
5 format(14x,'x',26x,'f(x)',23x,'F(x)',23x,'E(%)')
15 format(3(f25.14,2x),e25.15)
20 format(3(f25.14,2x),' - ')
stop " Fim "
end
c ##############################################################
function fat(n)
implicit double precision(a-h,o-z)
integer n
fat=dfloat(n)
do i=n,2,-1
xi=dfloat(i)
fat=fat*(xi-1.d0)
enddo
if(n.eq.0) fat=1.d0
return
end
c ##############################################################
Creio que o que tenho que mudar está nessa linha:
a(n)=(-1.d0)**i*b**(n-1)*sin(b*x0)**j*cos(b*x0)**k
Entendo pouco de série de Taylor, mas se me explicarem alguma coisa eu acho que entendo!
Desde já, Obrigado pela ajuda!


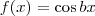 em torno de x0.
em torno de x0.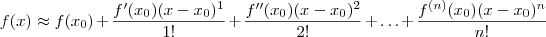

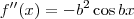
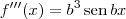
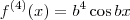
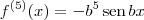
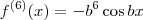
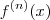 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
