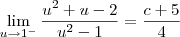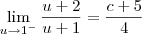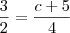por CaioLemos » Qui Mar 22, 2012 13:18
por CaioLemos » Qui Mar 22, 2012 13:18
Bom dia rapaziada, sou novo no forum e nao sei muito bem como editar as formulas, mas acho que dá para entender:
1-Determine o valor da constante C para que F seja continua em [0,

)
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
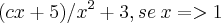
<=,=> Querem dizer maior ou igual
Bom, a minha dúvida é a seguinte: No primeiro momento, eu igualei a f(x)
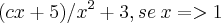
substituio x por 1para achar f(1), porem quando vo fazer o limite da
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
com X tendendo a 1, caio numa indeterminação 0/0. Minha idéia era achar o valor do limite
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
com X tendendo a 1 e dps igualar a F(1) para achar o C
Queria saber se o meu pensamento está correto e como sair da indeterminação
Obrigado
-
CaioLemos
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 22, 2012 13:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por LuizAquino » Qui Mar 22, 2012 15:59
por LuizAquino » Qui Mar 22, 2012 15:59
CaioLemos escreveu:1-Determine o valor da constante C para que F seja continua em [0,

)
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
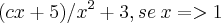
<=,=> Querem dizer maior ou igual
O que você escreveu é equivalente a:
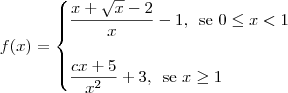
Mas eu presumo que a função original seja:
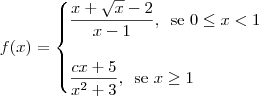
Se você desejava escrever algo assim, você deveria ter usado algo como:
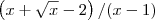
, se 0<= x <1
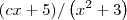
, se x =>1
Note a importância do uso adequado dos parênteses!
CaioLemos escreveu:Bom, a minha dúvida é a seguinte: No primeiro momento, eu igualei a f(x)
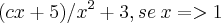
substituio x por 1 para achar f(1), porem quando vo fazer o limite da
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
com X tendendo a 1, caio numa indeterminação 0/0. Minha idéia era achar o valor do limite
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
com X tendendo a 1 e dps igualar a F(1) para achar o C
Queria saber se o meu pensamento está correto e como sair da indeterminação
Temos que:
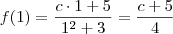
Desejamos determinar c de tal modo que:

Nós já temos que:
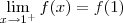
Falta agora:
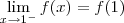
Desejamos então que:
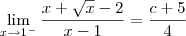
Há várias formas de resolver esse limite. Uma delas é usando a substituição
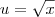
. Desse modo, quando
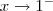
temos que
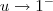
. Podemos então reescrever esse limite como:
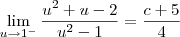
Fatorando os polinômios que aparecem no numerador e no denominador, temos que:

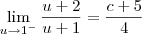
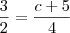
Agora basta terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por CaioLemos » Qui Mar 22, 2012 17:39
por CaioLemos » Qui Mar 22, 2012 17:39
LuizAquino obrigado pela resposta. Estava precisando dessa ajuda, obrigado mesmo!
-
CaioLemos
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 22, 2012 13:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite Continuidade
por Claudin » Sáb Out 01, 2011 11:33
- 10 Respostas
- 5808 Exibições
- Última mensagem por Claudin

Seg Out 03, 2011 10:37
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Thyago Quimica » Seg Mai 21, 2012 14:11
- 1 Respostas
- 1666 Exibições
- Última mensagem por LuizAquino

Ter Mai 22, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Raquel299 » Sex Abr 10, 2015 10:43
- 2 Respostas
- 1828 Exibições
- Última mensagem por Raquel299

Ter Abr 14, 2015 18:17
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Raquel299 » Ter Abr 14, 2015 20:58
- 1 Respostas
- 1477 Exibições
- Última mensagem por Cleyson007

Qua Abr 15, 2015 18:26
Cálculo: Limites, Derivadas e Integrais
-
- Limite- Continuidade em intervalos
por killerkill » Sáb Ago 13, 2011 02:25
- 7 Respostas
- 7948 Exibições
- Última mensagem por killerkill

Qua Ago 17, 2011 23:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 )
)![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
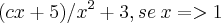
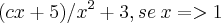
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png)
![f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1 f(x)= (\!x+\sqrt[2]{x}-2)/x-1 , se \:x<=x<1](/latexrender/pictures/39e46eb54f0ef49ad0383fcd1334a2c1.png) com X tendendo a 1 e dps igualar a F(1) para achar o C
com X tendendo a 1 e dps igualar a F(1) para achar o C

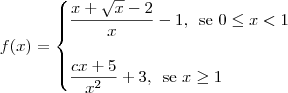
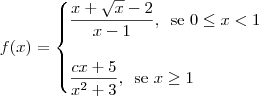
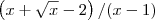 , se 0<= x <1
, se 0<= x <1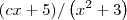 , se x =>1
, se x =>1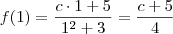

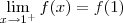
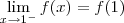
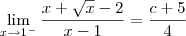
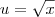 . Desse modo, quando
. Desse modo, quando 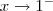 temos que
temos que 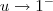 . Podemos então reescrever esse limite como:
. Podemos então reescrever esse limite como: